You go through life, and then you realise you only live once, and that there are some things you might have lost or given away when you were young, so you go back to find them.
[https:]]
Feeds
22090 items (21898 unread) in 44 feeds
-
Adhoc. Filosofia a secundària
(25 unread) -
Associació filosófica de les Illes Balears (98 unread)
-
telèmac
(1017 unread)
-
A l'ombra de Zadig.
(160 unread)
-
Aprender a Pensar
(181 unread)
-
aprendre a pensar (68 unread)
-
ÁPEIRON (16 unread)
-
Blog de Filosofía - Filosóficamente - Blog de Filosofía - Filosóficamente (23 unread)
-
Boulé (267 unread)
-
carbonilla
(45 unread)
-
Comunitat Virtual de Filosofia
(732 unread)
-
CONTRA LA NECIESA
(31 unread)
-
CREACIÓ FILOSÒFICA II (28 unread)
-
DE SOFISTA A SAVI
(10 unread)
-
DIDÁCTICA de la FILOSOFÍA
(41 unread)
-
Educación y filosofía
(229 unread)
-
El café de Ocata (4635 unread)
-
El club de los filósofos muertos (88 unread)
-
El Pi de la Filosofia
-
EN-RAONAR
(489 unread)
-
ESTÈTICA DE L'EXISTÈNCIA. (570 unread)
-
Filolaberinto bachillerato (209 unread)
-
FILOPONTOS (10 unread)
-
Filosofía para cavernícolas
(592 unread)
-
FILOSOFIA A LES TERMES
(164 unread)
-
Filosofia avui
-
FILOSOFIA I NOVES TECNOLOGIES (36 unread)
-
Filosofia para todos
(134 unread)
-
Filosofia per a joves
(11 unread)
-
L'home que mira
(74 unread)
-
La lechuza de Minerva (26 unread)
-
La pitxa un lio (9314 unread)
-
LAS RAMAS DEL ÁRBOL (78 unread)
-
Materiales para pensar
(1015 unread)
-
Meditacions des de l'esfera
(13 unread)
-
-
Minervagigia (24 unread)
-
No només filo
(61 unread)
-
Orelles de burro (498 unread)
-
SAPERE AUDERE
(513 unread)
-
satiàgraha (25 unread)
-
UN LUGAR PARA APRENDER FILOSOFÍA
(69 unread)
-
UNA CAIXA D´EINES PER PENSAR
(40 unread)
-
Vida de profesor
(209 unread)
«
Expand/Collapse
(8 unread)
-
21:34 Dolores
» telèmacAr dheis Dé go raibh a hanam.
You go through life, and then you realise you only live once, and that there are some things you might have lost or given away when you were young, so you go back to find them.
[https:]]
-
Poema amoroso
» El café de Ocata... I like to kiss you with tongue, with gusto
with socks still on. I love you like a vulture loves
the careless deer at the roadside.
...
- Traci Brinhall, "Love Poem Without a Drop of Hyperbole in It"
-
16:33
¿ QUÉ QUIERE DECIR "EJERCICIOS ESPIRITUALES PARA MATERIALISTAS ?
» Materiales para pensar
Escrito por Luis Roca Jusmet
Voy a intentar profundizar en el sentido de la expresión de la que, de alguna forma, me considero creador : "Ejercicios espirituales para materialistas." Aunque, como sabemos, la "creación" casi siempre es la metáfora de la "transformación". En este caso es evidente y no me las quiero dar de original. Simplemente he unido dos expresiones cuyo resultado es paradójico y hasta algo provocativo. Vamos analizarlo con detalle y empezaremos por el término "Ejercicio espiritual".
Como sabemos, la noción es conocida por su uso mayoritario, que es el que le dio Ignacio de Loyola. El fundador de la orden de los jesuitas propuso una serie de ejercicios vinculados a los preceptos católicos : entenderlos y aplicarlos a la vida cotidiana. Todo bajo la dirección de un director espiritual, es decir, un sacerdote.
En su libro "La filosofía perenne", publicado en 1945, Aldous Huxley dedica un capítulo a los "Ejercicios espirituales". En él consideraba que frente al culto público ( ritos, sacramentos, ceremonias ) los ejercicios espirituales se referían a la devoción particular. Huxley define los ejercicios espirituales como unas prácticas ascéticas ligadas a la oración y a la Realidad Divina. Tenemos entonces una idea religiosa de los ejercicios espirituales, aunque no vinculado exclusivamente a la tradición católica, como el hinduismo, el budismo o el islamismo. Pero es el filósofo francés Pierre Hadot el que le dará un giro al término al definir la filosofía antigua ( y la moderna en la medida en que ha seguido el espíritu original) como un ejercicio espiritual, es decir como una práctica transformadora del sujeto. El año 2003 publicará "Ejercicios espirituales y Filosofía antigua".
En esta línea Michel Foucault, en su curso de 1982 "Hermenéutica del sujeto" recogerá la idea y el término de Hadot. Finalmente, un filósofo francés seguidor de Hadot, Xavier Pavie publicará el año 2012 el libro "Exercicis Spirituels. Lecçons de la philosophie antique."
En otra línea, también inspirada por Hadot, Jean Allouch escribe el año 2007 "¿ Es el psicoanálisis un ejercicio espiritual ?".
¿ A qué me refiero cuando utilizo la palabra "materialista" ?
Evidentemente descarto de entrada la noción común que entiende por "materialista" aquel que solo se preocupa y ocupa de los bienes materiales. me refiero a la concepción filosófica. Voy a tomar como referencia el diccionario de Filosofía de Nicolás Abbagnano, publicado en 1961 ( la traducción española en 1963,FCE).
El primer sentido que apunta, y que es la base de mi formulación, es el cosmológico: el carácter originario e inderivable de la materia, que precede a todo otro ser y es su causa. Esta concepción tiene precisamente en la antigüedad como representante a Epicuro.
En esta línea quiero recordar la cita de un filósofo contemporáneo que abre el epilogo de mi libro : "El materialismo no es el que niega el espíritu , sino el que plantea que el espíritu, que no se reduce a la materia, está condicionado por esta."
¿ Qué quiere decir esta afirmación ? . En primer lugar que se niega cualquier Trascendencia a lo natural. Todo es inmanente, nada esta fuera del mundo físico. Negamos así las religiones que hablan de un Dios creador. En segundo lugar niega también las teorías espiritualistas que plantean que la materia es una expresión del espíritu o la conciencia. En tercer lugar niega también las teorías solipsistas, para las cuales la única realidad que conocemos es la mental.
Pero hay que entender que también niega los reduccionismos fisicalistas para los que lo espiritual es un falso nombre que en realidad habla de procesos materiales o físicos, como la connexión neural o determinados procesos neuroquímicos.
"Materialismo" es, por tanto, una palabra que afirma que estamos en un mundo físico y somo una realidad física, el cuerpo, que forma parte de él. Pero que los humanos somos capaces de producir unas realidades que no se reducen a lo material.
Ser materialista quiere decir que la única realidad es inmanente pero que la materia puede producir algo que llamamos "espiritual". Ejercicio espiritual es una práctica que puede por tanto crear algo "espiritual" en la materia.
Vamos a precisar más. Entiendo por "espiritual" todo lo que tiene que ver con valores éticos, morales y estéticos. Entiendo por "valores éticos" lo que permite proyectar la vida humana más allá del campo material de la necesidad y la satisfacción de la necesidad. Entiendo por "valores morales" lo que nos permite ir más allá de nuestra satisfacción y hacer lo que consideramos que es nuestro deber. Entiendo por "valores estéticos" lo que nos produce una satisfacción más allá del placer físico.
Justamente estos "ejercicios espirituales" son los que nos permiten transformarnos en sujetos éticos, morales y estéticos. Construirnos como tales. Esta es la óptica de Foucault. La de Hadot es la de transcender nuestro ego para abrirnos a lo universal ( la Humanidad, el Cosmos). la de hacernos más sabios, mejores y más justos. No necesariamente hemos de considerar estos dos planteamientos como contradictorios. Ambos se refiere a lo que he llamado transformación y espiritualidad. Ninguno hace referencia a una Trascendencia o Espiritualidad.
¿ Qué es lo que se transforma ? Se transforma la mente, pero la mente no es otra cosa, y aquí cito a Spinoza, que la idea del cuerpo. Los ejercicios son ejercicios de la mente. Pero deberían complementarse con ejercicios del cuerpo, como bien señala Foucault y parece olvidar Hadot.
[https:]]
-
Personalidad
» El café de Ocata"Personalidad": así titula Victor Serge la entrada de su diario del 25 de enero de 1943:Una mujer me dice: "Considero que este tipo de arte no vale nada, etc." Tengo ganas de responderle: "Está muy bien que piense, señora, pero sería mejor que pensara bien. Pues su pensamiento -admitiendo que eso sea pensamiento- no vale a causa de usted, sino usted la que debería valer a causa de su pensamiento".
Leo el texto un par de veces. La primera pienso que Serge está jugando un juego peligroso, a borde del narcisismo intelectual. La segunda, concluyo que es honesto, y eso me inquieta más, porque todo lo que aparenta honestidad tiende a ganar verosimilitud. ¿Es acaso realizable el programa intelectual y moral que propugna Serge? ¿Y, si no es realizable, por qué encontramos a tantos intelectuales bien intencionados y honestos que siente necesidad de defenderlo?En todas las cosas hay una verdad que no es de ninguna manera personal, que expresa necesidades independientes de nosotros y, por eso mismo, hay que esforzarse en comprender antes de hablar. El pensamiento superficial, que sólo es apariencia, simulacro, juego de conversación o una manera de colmar el vacío de uno mismo admirándose en un espejo intelectual de pacotilla, se complace oponiéndose a los conformismos con pequeños esquemas de pensamiento ya hechos. No inventa su propio pequeño conformismo y sólo alcanza a desarrollar un juego social poco interesante. La verdadera victoria sobre esta inercia (el conformismo) es el fruto del rigor desinteresado, impersonal, en el conocimiento de la realidad, la búsqueda de la verdad. Así se afirma una personalidad real.
¿La honestidad también puede ser una forma del conformismo que critica Serge? Recordar a Nietzsche, etc...
Todos nos rendimos más de una vez al día a la impaciencia de la opinión. A veces, nos rendimos criticando la impaciencia de la opinión.
Efectivamente, nuestro pensamiento no vale porque sea nuestro. El problema es que en la vida cotidiana no podemos pararnos a reflexionar si todo aquello que decimos es estrictamente verdadero...
¿Qué sería de nosotros sin todos esos pequeños conformismos que el hábito ha ido adhiriendo a nuestro lenguaje?
-
12:10
Más de mil tipos distintos de ramos
» Aprender a Pensar“Más de mil tipos distintos de ramos de rosas” es el lema de una floristería. Está escrito en letras grandes y llamativas en la cristalera de la tienda, para captar la atención de todas las personas que pasan por el exterior de la misma. Los ramos de rosas son su producto estrella. Estos están formados por doce rosas, las cuales pueden ser de color rojo, blanco, rosa, amarillo, naranja o azul, y la cantidad de rosas de cada color en un ramo cualquiera varía entre ninguna, cuando ese color no forma parte del ramo, y doce, cuando el ramo es monocolor. Los dueños de la floristería afirman que se pueden componer más de mil tipos distintos de ramos de rosas, pero ¿cuántos tipos de ramos distintos son exactamente?
Esta cuestión puede plantearse matemáticamente. Si llamamos x, y, z, r, s, t a las variables que nos indican la cantidad de flores de cada color (respectivamente, rojo, blanco, rosa, amarillo, naranja y azul) que puede haber en un ramo de rosas, la cantidad de ramos distintos que se pueden componer es igual a la cantidad de soluciones de la ecuación
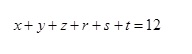
Una de las cuestiones interesantes de este problema matemático, calcular las soluciones de la anterior ecuación lineal, es que se puede resolver de una forma sencilla y hermosa, que consiste en sustituir las soluciones numéricas de la ecuación por diagramas de puntos y líneas, y contar cuántos diagramas existen.
Una solución de la ecuación anterior puede interpretarse como hacer seis grupos a partir de un conjunto de doce objetos. La cantidad de objetos de cada grupo representa el valor de cada variable, luego el número de rosas de cierto color en el ramo. En el diagrama se considera que los objetos son los puntos y se utilizan las líneas verticales para separar los seis grupos. Así, a la solución (1, 3, 2, 4, 1, 1) –que se corresponde con el ramo de una rosa roja, tres blancas, dos rosas, cuatro amarillas, una naranja y una azul– se le asocia el diagrama •|•••|••|••••|•|•. Es decir, las líneas verticales separan tantos puntos como el número correspondiente de la solución, dentro del total de doce puntos. De igual forma, la solución (5, 3, 2, 0, 2, 0) tiene asociado el diagrama •••••|•••|••||••|, (3, 1, 2, 3, 1, 2), el diagrama •••|•|••|•••|•|•• y (6, 3, 0, 0, 0, 3), ••••••|•••||||•••.
Por lo tanto, para generar cada diagrama debemos colocar un punto o una línea en los diecisiete (doce más cinco) «lugares» posibles, cinco huecos para las líneas y doce para los puntos. Como basta con determinar los lugares de las líneas, puesto que el resto serán para los puntos, la solución es la cantidad de formas en se pueden elegir cinco «lugares» dentro de los diecisiete posibles, cuestión clásica de la combinatoria, que nos dice que es el conocido número combinatorio 17 sobre 5, C(17,5),
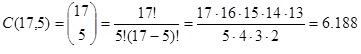
Por lo tanto, el número de tipos distintos de ramos de rosas posibles, con doce rosas que pueden ser de color rojo, blanco, rosa, amarillo, naranja o azul, es mayor de mil, exactamente 6.188 tipos distintos.
Este razonamiento, con diagramas de puntos y líneas, nos permite demostrar el resultado general (teorema) sobre ramos distintos de n rosas con hasta k colores distintos, o soluciones de la correspondiente ecuación lineal:
¿Qué solución de la ecuación lineal prefieres tú?
La entrada Más de mil tipos distintos de ramos se publicó primero en Aprender a pensar.
-
12:08
¿Cómo sacar partido al ábaco Soroban?
» Aprender a PensarJavier Bernabeu, editor del Equipo de Matemáticas de SM
Comenzaremos manipulando el ábaco, pasaremos a representarlo en las manos y acabaremos generando la imagen que nos permita realizar cálculos con la mente a gran velocidad. Todo ello en varios pasos, aunque lo primero es conocerlo. Te presento el ábaco Soroban.
Este ábaco está formado por una serie de varillas con piezas en ellas y una barra divisoria que delimita dos zonas. Una superior y una inferior. Para aprender a utilizarlo, sigue lo siguientes pasos, ilustrados por Macus Romero.
Paso 1. Juego libreAl igual que con cualquier otro material, debemos dejar al niño manipular el ábaco y jugar libremente con él. Ten en cuenta que los primeros minutos en los que el alumno se encuentra con un material nuevo va a explorarlo. Queramos o no lo vn a hacer, así que es preferible que reservemos un tiempo para que deje volar su imaginación…¡Encontrará muchos usos para su ábaco! Estas son algunas de las cosas que he visto hacer a los niños de 5 o 6 años en su primer contacto con el ábaco:
- Música, agitándolos como si fueran maracas.
- Echar carreras con ellos como si fueran coches con cientos de ruedas.
- Darse masajes unos a otros.
- Subirse encima y utilizar dos como si fueran patines.
Paso 2. ¿Está encendido tu ábaco?
Un ábaco no deja de ser una calculadora, por lo que lo primero que tenemos que hacer es encenderla. Al encender una calculadora pone cero. ¿Cómo podemos poner cero en nuestro ábaco? Asegúrate de que todas las piezas están alejadas de la barra divisoria y tu ábaco estará a cero. En el mundillo del ábaco se dice que “el ábaco está limpio”. Puedes alejarlas una a una o seguir estos sencillos pasos para ir más rápido:
- Pon de pie el ábaco de modo que todas las piezas inferiores caigan hacia abajo… ¡Las de abajo ya se han alejado!
- Apoya suavemente el ábaco en la mesa.
- Desliza el dedo índice por las piezas de arriba para alejarlas de la barra.
Si quieres que tus alumnos lo entiendan mejor, puedes consultar con ellos el siguiente vídeo:
Paso 3. Conocer el valor de cada pieza
De momento solo nos fijaremos en las piezas de la varilla situada más a la derecha. Cada pieza inferior tiene el valor uno y solo toma valor cuando las acercamos a la barra divisoria. Así representamos las cantidades del uno al cuatro.
- Si acercas una pieza habrás representado el uno.
- Si acercas otra habrás representado el uno y uno, que también se llama dos.
- Si acercas otra habrás representado uno y uno y uno o lo que es lo mismo dos y uno o lo que es lo mismo uno y dos. A cualquiera de estas representaciones la podemos llamar tres.
- Si acercas otra habrás representado cuatro unos o dos doses o un tres y un uno. A cualquiera de esas representaciones la podemos llamar cuatro.
- ¿Y si alejas todo? Pues habrás representado nada y a nada lo podremos llamar cero.
Es interesante que los alumnos verbalicen las cantidades de distintos modos. ¿Cómo puedes llegar al cuatro? ¿Cómo dices tres sin decir tres? ¿De qué manera puedes representar cuatro en un solo movimiento? ¿Y en dos movimientos? ¿Y en tres?
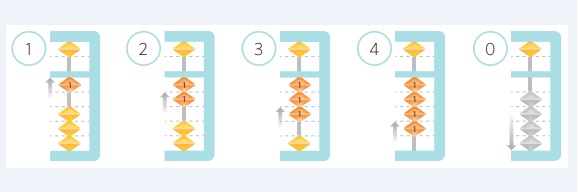
Si a tus alumnos no han comprendido bien cómo representar cantidades del uno al cuatro, diles que consulten este vídeo:
Paso 4. Identificar las pieza de abajo y de arriba
A las piezas inferiores se les llama bajocuentas o piezas de tierra. A cada pieza superior se le llama altocuentas o piezas del cielo.
La pieza superior tiene el valor cinco y solo tiene valor cuando la acercamos a la barra divisoria.
- Si acercamos únicamente la pieza superior habremos representado el cinco.
- Si añadimos una de abajo, habremos representado el cinco y uno. A cinco y uno lo podemos llamar seis.
- Si acercamos otra, tendremos cinco y uno y uno, que es lo mismo que cinco y dos o seis y uno, y lo podemos llamar siete.
- Si acercamos otra, tenemos el ocho.
- Y con otra más, tenemos el nueve.
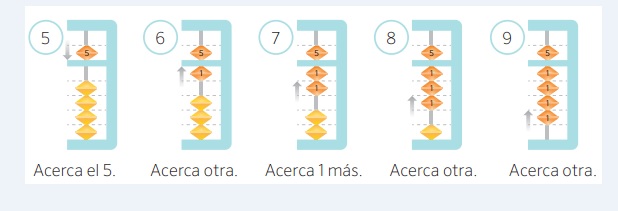
Paso 5. Busca el ábaco en tus dedos
Mira la palma de tu mano derecha. ¿Eres capaz de encontrar las piezas de valor uno? ¿Eres capaz de encontrar la pieza de valor cinco?¡Exacto! Tu mano derecha representa la varilla derecha del ábaco.
Uno Dos Tres
Cuatro Cinco Seis
Siete Ocho Nueve
¿Te apetece practicar un poco el cálculo mental con tus alumnos?
Una vez explicado el funcionamiento del ábaco, puedes proponer a tus alumnos darle al coco con ejercicios como estos:
- Llega al siete de tres formas distintas:
- Acercamos el cinco y el dos.
- Acercamos el seis y el uno.
- Acercamos el uno, el cinco y otro uno.
- …
- Si he llegado al nueve en tres movimientos, ¿qué he podido hacer?
- Acercar cinco, acercar dos y acercar dos.
- Acercar seis, acercar uno y acercar dos.
- Acercar nueve, alejar tres y acercar tres.
- …
Si no les ha quedado claro, comparte con ellos este vídeo:
La entrada ¿Cómo sacar partido al ábaco Soroban? se publicó primero en Aprender a pensar.
-
12:00
Grupo de Historia de las Matemáticas
» Aprender a PensarEspañol González, del Equipo de Coordinación del GHM/RSME
Este «Grupo especializado RSME» fue creado por la Real Sociedad Matemática Española el año 2015 como un instrumento para potenciar la historia de las matemáticas contemplando esa condición multidisciplinar que posee, concretada en sus enfoques propios interno y externo, en sus vínculos con la historia de ciencias y técnicas diversas, así como la lógica y la filosofía; en suma, la historia de las matemáticas es un magnífico puente entre las dos orillas de la cultura, la científica y la humanística. Este carácter se manifiesta de modo muy destacado en el papel que la historia de la más antigua de las ciencias tiene en su propia enseñanza.
Hipatia de Alenjandría, Pitágoras de Samos y Euclides fueron grandes mátemáticos del pasado.
El apoyo a los estudios históricos es uno de los síntomas de la madurez de las comunidades matemáticas en países del entorno europeo, situación a la que España se debe acercar. Los signos del alto nivel que prestigian a la comunidad matemática de nuestro país deben tener un correlato en historia de las matemáticas, lo que será posible evitando el declive que llegará si no se produce el relevo satisfactorio de la generación que desde finales del siglo pasado ha logrado que hoy sea un valor palpable la presencia internacional de la comunidad española de historiadores de las matemáticas. Pero la media de edad de las personas involucradas es elevada, lo que requiere prestar una atención muy especial a la promoción de jóvenes.
La historia de las matemáticas es ya un campo de investigación con su propia metodología, hace tiempo que no es cosa de aficionados; debe ser estudiada e investigada en nuestro país con método científico y rigor, de una manera reglada y sostenida, y tener un papel en la formación de los matemáticos y de los profesores de matemáticas. En este sentido, el balance actual es positivo pero insuficiente, falta cohesionar en red temática los grupos de investigación que existen diseminados y un programa formativo universitario en historia de las matemáticas. Hay que impulsar la presencia de asignaturas de esta materia en los grados y en los másteres, especialmente en el de profesorado, así como la realización de tesis doctorales proporcionando a los doctorandos un buen plan de formación específico. Conviene también diseminar cursos breves de diverso tipo con los que facilitar y orientar la formación básica en historia de las matemáticas a todos los interesados en ella y realizar divulgación de las matemáticas a través de su historia.
Bernhard Riemann y la matemática Emmy Noether han sido también figuras claves.
Otras iniciativas del GHM/RSME se relacionan con la historia de las matemáticas en el seno de la propia Sociedad, por ejemplo asesorando en la formación de su Archivo Histórico y colaborando en el mantenimiento y promoción de la «Sección de Historia» de La Gaceta de la RSME; también llevando a cabo actividades específicas dentro de los congresos bienales de la RSME y otros que celebra conjuntamente con sociedades matemáticas de otros países. El Grupo ha iniciado su andadura formado por personas que son socios de la RSME y otras que pertenecen a diversas sociedades científicas de ámbitos relacionados. Tiene un equipo de coordinación (véase «Comisiones, Comités y Grupos» en la entrada «La Sociedad» de la página web www.rsme.es), abierto a cualquier contacto para asuntos relacionados con la historia de las matemáticas.
La entrada Grupo de Historia de las Matemáticas se publicó primero en Aprender a pensar.
-
8:53
Activitat 8: Pressupòsits gnoseològics i criteri de veritat del racionalisme i l’empirisme moderns
» Comunitat Virtual de FilosofiaAl document adjunt teniu l’octava activitat del curs: Recordeu que la finalitat d’aquestes activitats és preparar amb antelació les possibles preguntes 4 i 5 de l’examen. La data límit de lliurament és el 23 de gener. L’haureu d’arxivar en el … Continua llegint →