
Escrito por Luis Roca Jusmet
Si seguimos las indicaciones de Nicolás Abbagano en su
Diccionario de Filosofía, podemos considerar que la diferencia entre
imaginación y
fantasía se basa en una distinción moderna establecida por los racionalistas franceses en su lógica de Port Royal, que pasan a considerar la fantasía como
una imaginación sin regla o freno. Kant, en esta misma línea consideraría que la fantasía es
la imaginación en cuanto que produce imágenes sin quererlo. Desde el polo opuesto, el romanticismo exalta la fantasía en su carácter de
imaginación creadora. Podemos constatar en todos los casos un elemento común, que es atribuir a la fantasía un carácter transgresor con respecto a las reglas ordinarias del conocer. Esta cuestión se valora negativamente desde una
epistemología realista en su versión más clásica, en la medida en que considera que se quiere sustituir el mundo real por otro irreal.
Pero lo que centrará mi trabajo teórico sobre
la fantasía es la vinculación que podemos establecer a través de ella entre las nociones de
imaginario, de
simbólico y de
deseo. La tradición psiconalítica es la que ha elaborado más esta noción de
fantasía, y esto desde el nuevo horizonte abierto por Freud hasta las brillantes aportaciones de Melaine Klein, Jacques Lacan o Jean Laplanche .
Se la concibe en esta línea
como un elemento estructurante de la vida del sujeto, en el sentido de que su actividad es la que modela y organiza el psiquismo desde el deseo. Para entrar en este planteamiento de
la fantasía y sus vicisitudes, nos orientaremos por lo que dicen Jean Laplanche y Jean-Bertrand Pontalis en su riguroso y clarificador
Diccionario de psicoanálisis. Lo primero que sugieren es la dificultad de traducción al francés del término alemán
phantasie ( que es el originario freudiano), porque éste tiene un sentido excesivamente amplio que le da una cierta ambigüedad, ya que se refiere a la vez a
la facultad y
al producto de la actividad. La traducción francesa elegida mayoritariamente es
fantasme, que le da al término una resonancia más limitada pero más específicamente psicoanalítica y que quedó plenamente consolidada por la corriente lacaniana ( en contra de la opinión de Daniel Lagache, que quería traducirlo por
fantasie, que refleja mejor para él este doble aspecto de
actividad creadora y de sus producciones). La definición propuesta por Laplanche y Pontalis es muy interesante: " Guión imaginario en el que se halla presente el sujeto y que representa, en forma más o menos deformada por los procesos defensivos, la realización de un deseo y, en último término,
un deseo inconsciente. La fantasía se presenta bajo distintas modalidades:
fantasías conscientes o sueños diurnos;
fantasías inconscientes que descubre el análisis como estructuras subyacentes a un contenido manifiesto, y
fantasías originarias."
La teoría psicoanalítica habla de lo que Freud llamaba
la novela familiar del neurótico, que es el resultado de la narración imaginaria que el neurótico se inventa sobre su historia familiar, es decir, que siendo una verdad-a-medias adquiere desde el punto de vista psíquico un peso absoluto en el psiquismo del sujeto. Los factores que intervienen en la formación de esta narración son variados: deseo edípico, confrontación con el progenitor del mismo sexo, rivalidad fraterna. Pero no sólo
el neurótico sintomático el que realiza esta novela imaginaria, sino cualquier ser humano en la solución subjetiva de
su devenir edípico. Esto nos lleva a la formulación radical del psicoanálisis, planteada por Freud y por Lacan, de cuestionar los límites entre
el sujeto psíquicamente normal y
el sujeto anormal, para acabar afirmando que todos tenemos una estructura clínica que, latente o manifiesta, siempre estará presente. La implicación es que incluso
los sujetos supuestamente normales tienen una estructura neurótica ( histérica, obsesiva o fóbica) perversa o psicótica ( esquizofrénica, paranoica o melancólica). La estructura puede manifestarse o no, según la determinación biografía de cada sujeto, pero desde esta planteamiento todos arrastramos, en mayor o menor medida, alguna ficción sobre nuestra propia historia familiar, que sería uno de los aspectos que configurará nuestra fantasía personal.
Laplanche y Pontalis son autores que han trabajado a fondo el tema del
estatuto ontológico de la fantasía a partir de la obra de Freud, sobre todo con su estudio sobre
las fantasías originarias , que para él tienen un carácter universal. Estas serían la de
la escena originaria, la de
la castración y la de
la seducción, cuya función es dar una respuesta al niño a los enigmas que se le presentan respecto a su propio origen (
la escena originaria fantaseada del acto sexual de los padres) a la diferencia sexual (
fantasía de castración de la niña) y del propio despertar de la sexualidad (
la fantasía de ser seducido por el progenitor del otro sexo). Son fantasías que funcionarían como una especie de esquemas que imponen su ley al imaginario y que son irreductibles a la experiencia individual. Freud parece considerar que las fantasías inconscientes individuales lo que hacen es llenar las lagunas de estas fantasías originarias universales, que por otra parte están sometidas a la represión originaria que constituirá las base del inconsciente. Serían una especie de
prehistoria mítica de la especie que se mantendría de forma inconsciente como huellas amnésicas heredadas; pero el problema que se le presenta a Freud es el de cómo justificar estas herencias arcaicas filogenéticas sin caer en la teorización de un inconsciente colectivo, precisamente en el momento en que sostiene la batalla teórica más dura con Jung. La explicación dada por Freud ( que no resulta convincente para Laplanche y Pontalis), es que deben ser comprendidas como
una prehistoria en la historia del sujeto, en el sentido de una preestuctura que es actualizada y transmitida por la fantasía de los padres. En todo caso es evidente que el niño fantasea sobre unas cuestiones que despiertan su curiosidad, que podemos aceptar que son a grandes rasgos las que define Freud, por lo menos en un marco cultural compartido.
Las definiciones que Freud va haciendo del término
fantasía a lo largo de su obra son variadas pero siempre se la considera como
una formación psíquica nuclear, sea consciente o inconsciente. Por un lado, nos dice, tenemos
fantasías inconscientes, que son el contenido primario y latente de lo que se manifiesta secundariamente en los sueños y en los síntomas de los histéricos, que se ocultan por la censura de la represión y sólo son accesibles de manera indirecta, a través de la construcción en el análisis. Por otro lado están
las fantasías conscientes, que van desde las ensoñaciones diurnas hasta las sexuales, cuya formulación más dura es la de los perversos. Pero Freud considera que las fantasías son básicamente inconscientes y este origen es decisivo para entender cual es su destino, ya que aunque son incapaces de volverse conscientes se aprovechan de este sistema para manifestarse por vía indirecta. También queda clara su relación compleja con el deseo ya que también aparecen en la narración mecanismos defensivos que lo distorsionan.
Freud tiene un texto paradigmático sobre la formación de la fantasía que es
Pegan a un niño, en el que Freud analiza un caso clínico de
fantasía de flagelación que padece una niña, y cuyo proceso se inicia entre los cinco o seis años. En la primera fase hay el un proceso asociativo que transforma una escena en la que
un padre pega a un niño en otra en la que
el padre pega al niño odiado por mí. La segunda fase implica la transformación de esta fantasía en otra que produce un goce masoquista y que muestra que
yo soy golpeada por mi padre. La tercera fase implica otra transformación importante, ya que
la persona que pega permanece indeterminada, ya no es el padre. Las últimas fantasías producen una intensa excitación sexual a la niña, que se resuelve con la masturbación. La pregunta freudiana es cual es el cambio a través del cual una fantasía sádica se transforma en una fantasía sexual masoquista. Sin entrar en los detalles me interesa aquí señalar que con este ejemplo clínico Freud muestra la continuidad entre fantasías conscientes e inconscientes, ya que en este caso la sujeto recuerda la primera y tercera fase y es la segunda la que cae bajo los efectos de la represión, precisamente porque es la que tiene un carácter incestuoso que sirve como enlace entre la primera y la tercera.
La fantasía es para el psicoanálisis uno de los destinos posibles de
la pulsión, que es el término que utiliza Freud para referirse a la versión humana del instinto, cuya característica es que no tiene un objeto específico y natural propio, El ser humano, que por sus características de desvalimiento esta completamente supeditado al
Otro Primordial ( la Madre), pierde este objeto esencial al entrar en el orden simbólico. El objeto de la pulsión es, por tanto, un objeto perdido ya que se refiere a
una especie de incesto mítico. El yo se opone entonces a la pulsión de tres maneras : con la represión, con la sublimación y con la fantasía y ésta última opción implica interiorizar el objeto prohibido distorsionando la imagen a la que está ligada; con esto la pulsión se orientará entonces hacia alguien que nos recuerde al objeto oculto de nuestra fantasía, sin que ni siquiera seamos conscientes de ello. Si recordamos la página introductoria de la famosa novela de Lawrence Durrell titulada
Justine hay una cita de Freud en la que dice que
en una relación sexual siempre intervienen cuatro personas. Lo cual quiere decir que aparte de las personas reales implicadas están las fantaseadas por sus participantes reales. En una de las mejores películas de Woody Allen,
Delitos y faltas, hay un viejo profesor judío de filosofía que tiene un magnífico discurso la imposibilidad del amor, en el que dice que las personas amadas nos recuerdan a los que amamos en nuestra infancia, pero a las que a la vez les exigimos corregir sus defectos y todo lo injusto que hicieron con nosotros. Creo que es una explicación muy lúcida de lo que puede ser la fantasía amorosa y también de
la imposibilidad de que la relación de pareja sea armónica ( que es lo que pretende decir Lacan con su provocadora expresión de que
no hay relación sexual).
Hay en Freud una búsqueda cada vez más insistente
del origen de la estructura y los contenidos de la fantasía y esto le lleva al estudio del mito, que más allá del planteamiento positivista ( que lo considera un estadio superado y primitivo del conocimiento humano) contiene siempre para él
un núcleo de verdad. Verdad que no es evidentemente de carácter fáctico sino de carácter psíquico, como es el expresado en su estudio “Tótem y tabú” donde
el Padre de la horda posee a todas las mujeres y tiene aterrorizados a sus hijos, que acaban uniéndose entre ellos para matarle.
La palabra
mito no es casual, ya que el contenido tiene clara relación con
el enigma de los orígenes, al que aporta una representación y una solución (es interesante constatar que los estudios históricos de Mircea Elíade confirman esta visión del mito como
modelo ejemplar sobre los orígenes)
. Aunque Freud acepta que biológicamente es insostenible buscar una fundamentación al mito, también considera que es necesario mantener una crítica radical a la teoría jungiana del
inconsciente colectivo, que se basa en una concepción de los arquetipos a los que se accedería a partir de
una imaginación creadora captadora de símbolos innatos y universales. A pesar de las dificultad de construir una teoría propia sobre estos mitos colectivos Freud recoge un material muy rico, relacionado básicamente con la religión, pero también con la tragedia ( Edipo, Electra, Antígona) o con el drama ( Hamlet). Lacan.elabora un estudio muy interesante sobre este último
y más en general sobre
el mito individual del neurótico, que define de la siguiente manera :“ Una cierta representación objetivada de una gesta que expresa de modo imaginario las relaciones fundamentales características de cierto modo de ser humano en una época determinada; si lo comprendemos como la manifestación social latente o patente, virtual o realizada, plena o vaciada de su sentido, de este modo de ser, es indudable que podemos volver a encontrar su función en la vivencia misma de un neurótico”
Jacques Lacan toma como referencias para esta formulación el ejemplo del
Hombre de las ratas, que es el ejemplo freudiano paradigmático de una neurosis obsesiva, y también del de Goethe, que extraerá de sus escritos autobiográficos. En ambos casos, dice, hay unos elementos comunes que adquieren un carácter mítico y sobre los que desarrollan su neurosis particular. Estos cuatro elementos, que también reflejan la actitud existencial del hombre moderno, son:
el Padre,
la Madre,
el Yo ( la relación narcisista) y
la Muerte.
Hay que hacer también una breve referencia a otra gran psicoanalista, Melaine Klein, que también da a
la fantasía un lugar clave en su teoría. Para ella las fantasías inconsciente son determinantes del estado psíquico del sujeto y la expresión mental de sus pulsiones, que buscan un objeto en el que concretarse. La fantasía. adopta también según su análisis la función de activarse como un mecanismo de defensa que se pone en marcha contra peligros internos, que pueden ser emociones negativas o incluso otras fantasías de carácter destructivo
. Laplanche y Pontalis consideran que aunque Melaine Klein asigne un papel muy importante a la fantasía no por ello deja de plantearlo en un término convencional, ya que las considera que pueden actuar como percepciones falsas de los objetos, por lo que nos separan del mundo real. Tenemos entonces con Melaine Klein ( y por supuesto en el psicoanálisis más convencional) una línea que sigue la formulación básica de Sartre : la percepción debe separarse de lo imaginario en nuestro conocimiento de la realidad.
Pero para Laplanche y Pontalis, así como para Castoriadis y Lacan, esta separación entre
percepción, por un lado, y
fantasía, por otra, no aparece tan clara por
el papel configurador del imaginario en la propia interpretación de la percepción.
El tema de
la fantasía es una de las problemáticas privilegiadas de Jacques Lacan, ya que recorre transversalmente muchos de sus seminarios y
Escritos, siendo el centro absoluto de uno de ellos,
Kant con Sade, donde llega a formalizarla en una fórmula que la relaciona con
el sujeto dividido y con el llamado
objeto a. No voy a explicar lo que significan ambos términos en el discurso lacaniano porque este trabajo no es una introducción a Lacan, pero sí hacer una breve aproximación para que podamos entender de lo que hablamos. Partimos de una paradoja, que es que
el sujeto es anterior al Orden simbólico y al mismo tiempo es su efecto. Cuando constituimos este Orden simbólico, perdemos nuestra realidad natural y dejamos de ser un organismo biológico para pasar a constituirnos como ser hablante, con lo cual quedamos constituidos como sujetos de la enunciación. Hablamos de lo que nos pasa, de lo que tenemos e ilusoriamente de lo que somos, ya que nuestro ser, que es la sustancia natural, lo perdemos con la alineación que implica entrar en el mundo del lenguaje, que es el del
Otro simbólico. Quedamos atrapados en este
Otro simbólico, ya que nos inscribimos en un mundo de significaciones ( que es el de la lengua, la ley y la familia en una determinada línea de filiación) que nos conduce a ocupar un lugar establecido. Pero esta inscripción en el orden simbólico no es absoluta, ya que queda
un resto, que es lo que Lacan llama
el objeto a ( a del
autre de
pequeño otro) y que es lo más singular y la causa de nuestro deseo, el sujeto del deseo que de alguna manera recoge lo que es anterior al lenguaje. El orden simbólico tiene la función de posibilitarnos construir la realidad a través de un discurso simbólico que habla de ella, porque nos separa de
lo real, que es lo traumático insoportable que el sujeto humano no puede asumir en su socialización, que no puede tolerar y que le produce angustia. El
objeto a, que es lo que queda de
lo real, es dónde se sitúa el núcleo de nuestro goce y también
el agujero alrededor del cual gira la pulsión. Aquí hay que entrar en la diferencia lacaniana entre
goce y
placer, en la que éste último, siguiendo a Freud, significa la eliminación de la tensión, ya que todo organismo busca su homoestasis, es decir, un equilibrio mínimo sin perturbaciones desagradables. Pero Freud constatará ( sobre todo a partir de los dos textos “Más allá del principio del placer”y “El problema económico del masoquismo”) que el sujeto humano busca la excitación y también la repetición, aunque le produzca dolor. El término que introducirá Freud a partir de esta reflexión será el de
pulsión de muerte, como tendencia a la repetición y, paradójicamente, a la aniquilación de lo vivo para pasar a un estado de reposo absoluto. Pero el mismo Freud constatará falla en esta formulación, ya que lo que buscan los humanos en la sexualidad no es la eliminación de la tensión sino la estimulación y la excitación, que ya es opera como una fuente de satisfacción. Lacan introduce la noción de
goce (
jouissance en el original francés ) para referirse a una satisfacción del exceso puede estar vinculado al dolor y en su límite a lo insoportable. El filósofo esloveno. Slavoj Žižek, va más lejos al
identificar el goce con la pulsión de muerte, dando a este término un sentido nuevo, con lo que nos encontramos con este
goce absoluto que buscamos y que hemos perdido al inscribirnos en el lenguaje no ha existido nunca, con lo cual perdemos algo que solo tenemos como un efecto retroactivo. En realidad la pérdida que lo constituye sólo puede entenderse desde la dimensión simbólica:
el símbolo es justamente una presencia hecha de ausencia. En esta línea Lacan trabajará lo que ha aprendido de Jackobson: los mecanismos básicos del lenguaje son la condensación y el desplazamiento, de las que surgirán la metáfora y la metonímia. En realidad Freud ya había hablado de estas figuras, pero dándoles una relación inversa, ya que para Freud el desplazamiento da lugar a la metáfora y la condensación a la metonimia. Lacan, afinando en el tema a partir las aportaciones de la lingüística, considera la cuestión con este matiz de diferencia. La metáfora es entonces una condensación, donde colocamos la parte en el lugar del todo porque es la sustitución de una palabra por otra. La metonimia es un desplazamiento en la que vamos de un lugar a otro porque es la conexión de una palabra con otra y en la primera el
sentido se produce a partir del sinsentido, ya que hay
una sobreimposición de significantes que mantiene un hilo de continuidad. Y aquí Lacan saca conclusiones fundamentales sobre el psiquismo humano relacionadas con
la cuestión de la falta, consecuencia de la represión, que es la que posibilita el deseo, como producto del límite establecido por la anterior. La inscripción del ser humano en el Orden simbólico lo transforma en un sujeto divido, ya que por una parte es consciente y por otra inconsciente, que es adonde apunta finalmente el deseo, que es la diferencia entre lo que lo que pedimos ( la demanda ) y lo que encontramos ( que no se corresponde nunca con el objeto imposible que buscamos ). Lo que posibilita y hace indestructible al deseo es que su objeto en el fondo está vacío, ya que su única existencia posible es ir desplazándose de un objeto a otro sin satisfacerse nunca plenamente, ya que siempre es
deseo de Otra Cosa. Y paralelamente a esta metonimia del deseo, que se va desplazando de un lugar a otro, están las metáforas del inconsciente ( síntoma, sueño) que lo que hacen es colocar un significante en el lugar del otro, que está reprimido.
Esbozando este proceso es como podemos entender el lugar nuclear que da Lacan a la fantasía, que nos proporciona un escenario imaginario que articulan lo simbólico y
lo real. La fantasía tiene elementos imaginarios que se articulan simbólicamente con significantes y siguiendo las reglas del lenguaje y en el que está presente
lo real ( ya que
el objeto a es su resto, que no es ni simbolizable ni representable). Pero el deseo se sostiene en la fantasía porque lo que hace ésta es encerrar el sujeto en
el objeto a, porque lo que hace es transformar el goce en placer adecuándolo al deseo. A partir de aquí Lacan formula su noción de
la fantasía fundamental , que tiene la función de dar a cada ser hablante una respuesta inconsciente frente al trauma y al vacío con el que nos encontramos al inscribirnos en el orden simbólico y enfrentarnos al enigma del
deseo del Otro ( ¿ que quiere de mí mi Madre, cuya mirada me dice que quiere algo que no le puedo dar ?). Lo que hay de insoportable en nuestro deseo es justamente lo que nos pone en contacto con este resto cuya proximidad con
lo real traumático nos produce angustia. Pero lo mismo que nos angustia es lo que posibilita el deseo,
el objeto a, aunque sea siempre su causa innombrable. La fantasía cubre el espacio vacío dejado por el objeto natural perdido, que nos permite reconstruirla desde esta
Otra escena. Sólo podemos acceder una realidad articulada por el lenguaje y necesitamos una fantasía desde la que elaborar la ficción que nos permita simbolizarla.. La realidad se sostiene, en algún sentido, desde esta
Fantasía fundamental, ya que la verdad del sujeto está en el inconsciente y no en el yo, que es una pura construcción imaginaria, una ilusión. Esto es lo que Lacan defiende en su ética, en su
no ceder al deseo, en su llevar al yo donde está
el Ello ( en contra de la interpretación convencional del psicoanálisis ortodoxo de llevar
el Ello donde está el yo.
La fantasía tiene en la tradición psicoanalítica las características siguientes: hay una escena y unos personajes (el papel del sujeto puede ir cambiando de rol) que desarrollan una acción que se manifiesta a través del verbo empleado y que se asocian a una parte delimitada del cuerpo, que son los bordes, el resto del goce del viviente que perdemos al entrar en la mediación de la palabra. El lenguaje nos ha vaciado de goce y éste solo queda en los bordes del cuerpo, en las zonas erógenas donde aparece una pulsión sin objeto. Pulsiones que formulamos a través de la demanda simbólica., en unas imágenes que se articulan en un argumento perverso ( que es diferente del argumento de un perverso, porque éste lo concreta en el mundo real) que en la medida que es consciente produce vergüenza y es vivido como algo que nos llega de forma extraña e involuntaria.y que produce afectos ambivalentes de placer y sufrimiento.
Slavoj Žižek desarrollará, a partir de la teoría lacaniana, toda una elaboración que vincula a ejemplos concretos y a situaciones actuales. Lo primero que señala es la
necesidad de mantener este espacio vacío, que es el que nos separa de
lo real y nos permite nuestra construcción simbólica de la realidad
56 desde la cual ésta puede ser formulada y asumida. Es decir, que la fantasía no es por tanto una forma de escapar a la realidad, sino, por el contrario, una forma de posibilitarla al permitir separarnos de lo real insoportable. Žižek considera que
la fantasía fundamental de cada sujeto es
el mito primordialmente reprimido57, que es una sombra espectral y no un conjunto de ensoñaciones diurnas vinculadas a nuestras formulaciones simbólicas y que nos permiten soportarlas. La fantasía, nos dice, representa
el pecado del goce y al mismo tiempo la narrativa mítica de cómo éste se perdió. Para entender mejor lo que quiere decir utilizaré un ejemplo concreto utilizado por el mismo Slavoj Žižek nos propone: hay una ensoñación masculina, nos dice, y que además es visible en el cine, que consiste en representar a la mujer como una máquina sexual, mientras que la ensoñación femenina es, por el contrario, la de un macho animal.
La fantasía sexual masculina quiere que la mujer sea un objeto sexual y
la fantasía sexual femenina quiere un macho potente que la satisfaga. Pero esta ensoñación de cada sexo por su lado, dice Žižek, simplemente complementa la ideología de que es posible una relación sexual armónica. Pero lo reprimido aquí es lo que es insoportable, que es la imposibilidad de la relación sexual armónica y en este sentido la fantasía reprimida es imaginarse la pareja ideal como un simio copulando con una cibermujer. Slavoj Žižek utiliza también el ejemplo de la última película de Stanley Kubrick,
Eyes Whide Shut, para poner de manifiesto el carácter ilusorio de la fantasía, ya que su realización no lleva a un éxtasis sino más bien a una experiencia vacía y fatua. Experimentar la fantasía sirve para ver su esterilidad : la sofisticada orgía colectiva es totalmente aséptica. Como dice Žižek, atravesar la fantasía sólo sirve para manifestar su estupidez.
En “Los siete velos de la fantasía”
la presenta a través de la metáfora de los siete velos: El primer velo nos muestra que
la posición del sujeto en la fantasía es la de ser sólo el sujeto de la enunciación, que es el sujeto vacío que la explica.. No tiene porqué ser además el protagonista de la narración, ya que el sujeto que fantasea no tiene porque coincidir no con el protagonista, el yo del enunciado. El segundo velo que presenta es que
la fantasía no es la proyección del deseo sino la condición que lo hace posible, por lo que la escena que monta la fantasía no es la de la satisfacción sino la de la construcción del deseo. A través de la fantasía aprendemos a desear, ya que su espacio tiene que dejar un vacío en la medida en que posibilita el deseo, cuya condición es la falta. El tercer velo que
la fantasía que tiene un carácter intersubjetivo radical,
ya que el Otro siempre está implicado, ya que
el objeto a, causa del deseo, es el núcleo de la fantasía es el que me hace percibirme como digno del
deseo del Otro. La pregunta original alrededor de la cual se articula la fantasía no es ¿ Qué quiero yo ? sino ¿
Qué quieren los otros de mí ? la fantasía es mi respuesta al enigma, al enigma de qué soy para los otros. Lo que fantaseo es lo que
el Otro ve en mí, es decir, su deseo. El cuarto velo que
la fantasía siempre tiene un carácter narrativo, que contamos para ocultar el antagonismo reprimido, la ruptura radical de
la Unidad originaria. El quinto velo muestra que
lo que es importante en la narración de la fantasía no es que tenga un carácter transgresor sino la propia instauración de la ley, el acto mismo de lo que llama la castración simbólica, que es la aceptación de la pérdida primordial que permite la constitución del Sujeto, su entrada en el orden simbólico. El sexto velo plantea que
lo que encontramos siempre en la fantasía es una mirada imposible porque el sujeto es a la vez el que mira y el que es mirado. El séptimo velo dice que
la fantasía debe ser implícita, debe mantener una distancia con la textura simbólica que la sostiene, lo cual quiere decir que siempre es una mentira. Aquí podemos incluir al arte como fantasía, en cuanto que hay una distancia, en cuanto que la obra artística no se presenta como real.
Otro tema interesante que plantea Žižek es la relación de la fantasía con la realidad virtual del ciberespacio. En un artículo titulado “¿Es posible atravesar la fantasía en el ciberespacio?”
desarrolla el tema de una manera muy sugerente, ya que Slavoj Žižek cuestiona el tópico de que el ciberespacio sea el universo posible para la realización de nuestras fantasías más íntimas. Precisamente para Žižek lo que pone de manifiesto el ciberespacio es que el ser humano ha perdido su ser, su sustancia vital al integrarse en el orden simbólico, el
Gran Otro y por esto no es extraño, continua, que la mayoría de fantasías que se ponen en escena sean masoquistas, ya que se trata de sentirse vivo a través del dolor. Y también que sean pasivas, ya que en este lugar que es el ciberespacio no somos un agente libre y espontáneo, como podría parecer porque siempre estamos a merced del
Otro, ya que la interfaz está totalmente determinada, porque que mi relación con el otro siempre está mediatizada por la maquinaria digital interpuesta ( que es la que ocupa el lugar del
Gran Otro que genera también un orden simbólico, aunque sea con una estructura laberíntica, Ahora bien, continua Žižek, lo que sí nos permite el ciberespacio es atravesar nuestra fantasía, en el sentido de que si nuestra
fantasía fundamental es inaccesible ( no podemos hablar de ella) el ciberespacio nos permite escenificarla y ganar alguna distancia con respecto a ella. Y este atravesar
la fantasía fundamental es, de alguna manera el objetivo del psicoanálisis, ya que distanciarnos de ella significa liberarnos de su determinación y dejar de ser un esclavo de ella. Žižek plantea otra vez que la categoría de
lo real tal coma la usa es justamente lo opuesto a la realidad, ya que la realidad social, que es la única posible, se sostiene en una ficción narrativa, en una fantasía social. Por lo tanto también nuestra percepción de la realidad está condicionada por la fantasía, que es quién decide que es la realidad y ésta no es lo que está afuera sino lo que uno constituye como tal: lo no aceptado, el resto, esto es
lo real.
Cornelius Castoriadis, por su parte, nos plantea, una doble batalla respecto al tema de la fantasía. Por una parte contra los supuestos planteamientos realistas que van desde Sartre hasta las principales corrientes psicoanalistas, desde la llamada psicología del yo hasta Melaine Klein. Recoge la aportación de Laplanche y Pontalis pero les critica su poca radicalidad y su incapacidad para entender
la actividad fantaseadora como producto del
imaginario radical, que es la única raíz de todas nuestras representaciones, incluida la percepción. Para él no tiene sentido contraponer
la percepción a
la fantasía porque ambas surgen de la misma matriz psíquica, que es el flujo que configura las representaciones, acompañadas siempre de un afecto e insertadas en un proceso intencional. La impresión de los sentidos se convierte en percepción-representación en función de una elaboración compleja que surge de este
imaginario radical de la psique y las fantasías participan también de este proceso como huellas de nuestras percepciones anteriores.
Castoriadis recoge la expresión freudiana de
fantasías compensadoras del deseo para nombrar las fantasías conscientes ( la religión, el arte ...) que intentan compensar esta
falta primordial del ser humano. Castoriadis considera que ésta surge de la carencia de algo que tuvimos y que nos dio plena satisfacción. Pero éste es uno de los puntos centrales en que Castoriadis diverge también radicalmente con Lacan y sus seguidores al considerar que
esta falta no tiene ninguna relación con el significante ni con un objeto perdido. Castoriadis no está de acuerdo con el papel determinante que Lacan da a la lingüística y considera que en ningún caso puede aceptarse que el inconsciente está estructurado como un lenguaje. No es el inconsciente, dice Castoriadis, el que funciona como un lenguaje, sino el consciente y el preconsciente. y los tres están atravesados por
el imaginario radical. Es absurdo, dice, querer entender el inconsciente desde las reglas de la lógica y la lingüística ( la metáfora y la metonimia), ya que ambas son una formalización del funcionamiento psíquico y no sus elementos constitutivos. Tampoco acepta que esta carencia básica del ser humano sea resultado estructural de un objeto perdido, como dice Lacan, y no porque no halla falta sino porque no hay objeto perdido, ya que lo que se ha perdido es un estado, que sería el de la fusión originaria en el Todo, con el que formamos primordialmente una
Unidad indiferenciada ( Mónada psíquica).. Para Castoriadis la separación entre el afuera/ adentro es un mecanismo defensivo que se va estableciendo desde el imaginario, con lo cual inicialmente el exterior es vivido inicialmente como una cloaca en la que tiramos lo que no queremos, lo que no toleramos en nuestro interior. Son creaciones imaginarias, parciales, en las que poco a poco se va estableciendo el esquema triádico: sujeto, objeto, otro. A partir de aquí Castoriadis desarrolla una crítica a la teoría lacaniana del deseo, remitiéndose inicialmente a Platón para recordar que, tal como dice éste en
El Banquete, se puede desear también aquello de lo que no se carece, en el sentido de querer mantenerlo. Por lo tanto, en contra de lo que dice Lacan, el deseo no remite exclusivamente a la carencia, a la falta, y es siempre la búsqueda de satisfacción de algo que ya hemos tenido y a lo que queremos volver, por lo que presupone siempre una imagen, ya que para existir tiene que haberse realizado con anterioridad.
El deseo absoluto, continua Castoriadis, es el de volver a este estado anterior a la primera separación, como nos recuerda
la nostalgia de lo orígenes que Mircea Elíade muestra a lo largo de su obra en los mitos e incluso
la continuidad del ser que Georges Bataille descubre tanto en lo sagrado como en el erotismo
61. Pero también hay que considerar la crítica que hace Freud a la búsqueda ilusoria de
estados oceánicos ( de disolución del sujeto) cuya función no es otra que la de encontrar una salida (regresiva) para evitar el dolor. Aunque Freud quizás no compartiría plenamente este punto de vista sí le daría la razón en dos aspectos: En primer lugar en que originalmente el yo incluye todo; luego, desprende de sí un mundo exterior.
. En segundo lugar en que la vida psíquica la conservación de lo pretérito es la regla.
A partir de estas teorizaciones Castoriadis concluye que en la fantasía el sujeto no ocupa un lugar en la escena fantaseada porque se identifica con toda la escena en su totalidad,, ya que ella misma representa en su conjunto esta
Unidad. Estas
fantasías compensadoras de carácter consciente son sobre todo las elaboradas desde el imaginario social: creaciones imaginarias que permiten una salida a partir de la sublimación de las pulsiones (arte, religión...) y que en caso de fracaso conduce a las salidas privadas (neurosis). Pero lo que no acaba de explicar es cual es la relación entre las pulsiones sexuales que hay que sublimar con este deseo de recuperar el estado perdido:
la Unidad orginaria. Para Lacan y sus seguidores el vínculo es tan contundente como perturbador: esta supuesta unidad no es otra cosa que
el Goce del Otro, de carácter mítico, que es el de
una relación sexual incestuosa imposible. No hay
Unidad perdida porque no siquiera ha existido una originaria fusión con
la Madre, ya que ésta siempre ha estado marcada por una ausencia, ya que un deseo apunta siempre a otro lugar como el niño percibe frente a
la Madre.
Quizás podríamos definir
la fantasía, siguiendo la sugerente expresión de Mannoni, como
la Otra escena de nuestro psiquismo, puesto que, consciente o inconscientemente es
la red desde la cual damos una significación emocional, desiderativa a las percepciones y por lo tanto, desde la que construimos la realidad. Lo que aporta la tradición psicoanalítica, desde Freud a Castoriadis, pasando por Meliane Klein y Jacques Lacan es muy interesante pero no dejan de ser especulaciones, que como tales son muy discutibles.
La metapsicología de Freud, como el mismo reconoce, es una construcción teórica no directamente contrastable, desde la que explicar los procesos mentales que generan la conducta. Freud se centra, por otra parte, en las fantasías sexuales y sobre ellas aporta análisis imprescindibles pero quizás con este enfoque reduccionista limita el campo de la interpretación de la fantasía. También Jacques Lacan y Melaine Klein son dos mentes brillantes que desarrollan líneas muy radicales en un sentido profundo pero parcial. Estos dos psicoanalistas son, sin duda, los que han aportado a esta tradición elementos más creativos y sugerentes. Pero han generado escuelas que precisamente por ser lo que son caen en el dogmatismo y en el sectarismo, aunque sin negar que también han producido estudios y análisis que merecen tenerse en cuenta. En el caso de la tradición lacaniana hay una reflexión filosófica polémica pero muy potente que es la del ya repetidamente citado Slavoj Žižek.
No hay que ceñirse por tanto de manera exclusiva a la perspectiva psicoanalítica sobre la fantasía, aunque continuo afirmando que es la que realiza los trabajos teóricos más interesantes sobre el tema. A Castoriadis también hay que tenerlo en cuenta de manera crítica porque
el imaginario radical es la supuesta clave absoluta para entenderlo todo y volvemos otra vez a la pretensión desmesurada de pretender haber descubierto la fórmula mágica a partir de cual crear un sistema teórico completo.
Aunque Castoriadis es muy interesante en sus argumentaciones no deja de ser reduccionista en sus conclusiones, tanto en su teoría del
imaginario radical como en la de
la Unidad originaria perdida. Hay en los dos casos ( el de Lacan y el de Castoriadis) una doble intuición muy penetrante, que es la del papel
del sentimiento de falta en el ser humano y la existencia de
un deseo que nunca acaba de satisfacerse. Lo que ocurre es que esta realidad, tan profunda y compleja, no tiene una respuesta definitiva como la que pretende dar cada uno de estos autores. Podemos concluir, esto sí, que
la fantasía es una creación simbólico-imaginaria que tiene que ver con esta carencia, que quiere cubrirla de alguna manera.
Hay una última aportación, imprescindible, vinculada al psicoanálisis pero regulada desde los descubrimientos de las neurociencias, que es la de Ansermet y Magistretti. Plantean que la percepción deja
una huella que se transforma en imagen mental ( del que dirán, por influencia lacaniana que adopta el papel del significante); que sigue una dinámica propia que lo puede alejar completamente de la percepción inicial. Es a partir a partir de este proceso que se va tejiendo la red de las fantasías, tengan éstas un carácter consciente o inconsciente. En nuestra relación con el mundo tenemos percepciones que nos conectan con el entorno en el que estamos insertos y al mismo tiempo hay una información interna que nos llega desde nuestra mente y que parte de nuestras fantasias y que da un significado emocional a lo que percibimos. Aquí salgo del psicoanálisis para continuar con otra aportación de la neurociencia, la de Antonio Damasio, que plantea que hay en nuestra mente
un depósito de conocimiento, que es el que hacemos valer en nuestra interpretación de las percepciones y que debe mantenerse separado del de la fantasía. Este depósito está formada, igual que la propia fantasía, y desde un punto de vista neuronal, por lo que él llama
unas representaciones disposicionales, que es la potencialidad latente que nos permite construir ideas y pensamientos desde las que entender lo percibido.
En todo caso
la vida humana está tejida de fantasías que vienen a ser guiones imaginarios a la vez que simbólicos, ya que aunque son básicamente imágenes tienen algo de narrativo, de lingüístico. Estos
guiones imaginarios no tienen que ver únicamente con el deseo sino también con la ley por lo que tienen de imperativo para el sujeto. El erotismo, entendido como lo que la sexualidad humana tiene de singular, está vinculado al imaginario y a la fantasía. Esto es cierto en un sentido social
porque hay un imaginario colectivo y fantasías más comunes en el seno de cada sociedad y que lo diferencia de lo biológico, de lo natural. Pero también hay algo de singular que está vinculado a
este resto que deja la socialización en cada sujeto. Freud ha insistido en la importancia de la sexualidad y ha considerado las fantasías como relacionadas con ella y aquí recoge uno de los aspectos que el ser humano tiene de más extraño, de más peculiar.
¿ Porqué la sexualidad, que es una inclinación biológica, tiene este poder sobre la condición humana ? ¿ Porqué el deseo como producto social está tan vinculado a la sexualidad ? ¿ Porqué las fantasías humanas son básicamente sexuales ? En todo caso Freud es muy certero cuando define
la pulsión como algo que está en la frontera entre lo somático y lo psíquico y Lacan también nos da una pista cuando nos dice que
la entrada en el Orden simbólico nos deja un agujero que deja un círculo alrededor de las zonas erógenas.
La función de lo simbólico es construir una estructura social a través de la lengua y de la institución social y
esta estructura es una red solidificada, dura, en la que nos inscribimos y que interiorizamos y nos permite un vínculo con el mundo humanizado. Es el
Otro simbólico al que nos anclamos una vez perdido el
Otro primordial,
la Madre.
El imaginario social son estas creencias que va tejiendo el orden simbólico en un marco social determinado y que van constituyendo una ideología, que viene a ser una fantasía social. Pero es la dimensión subjetiva del imaginario y de la fantasía la que me parece que tiene más interés porque es la red fluida en la que vamos tejiendo nuestros deseos, que es lo que nos mueve, lo que nos hace salir de la pasividad. Esta red es necesaria pero tiene sus peligros porque puede convertirse en un obstáculo cuando nos conduce a la ilusión o delirio o cuando nos encierra en el círculo vicioso del narcisismo.


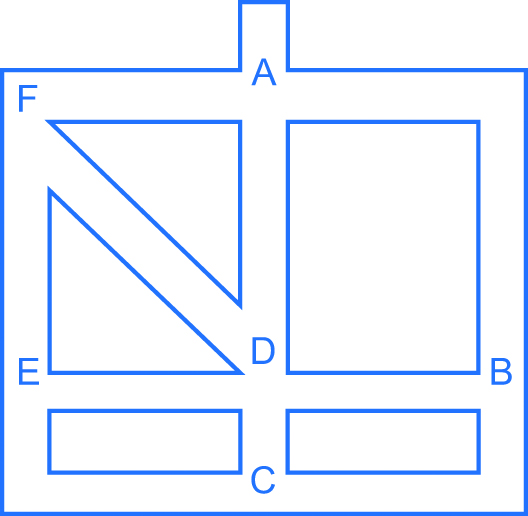 Laberinto.
Laberinto.
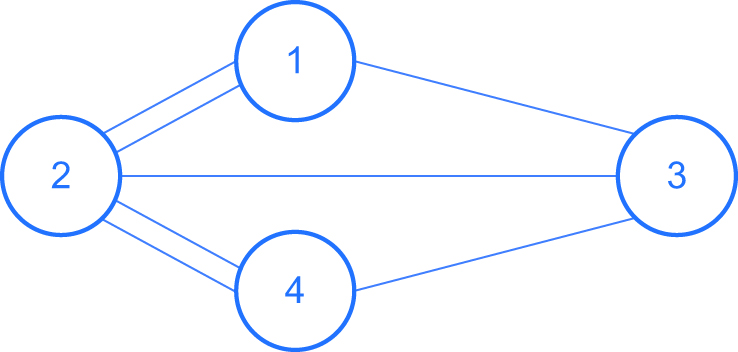
 Representación del laberinto como grafo.
Representación del laberinto como grafo.
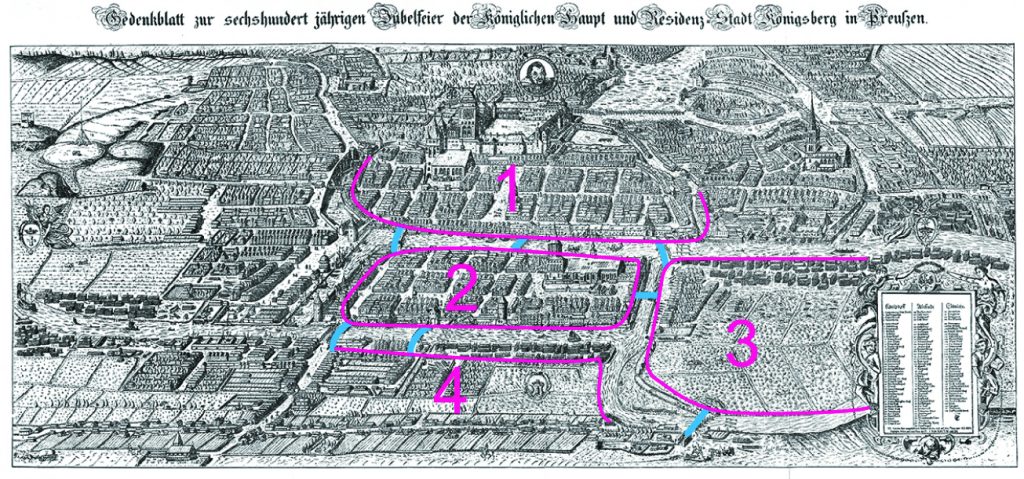 Los puentes de Königsberg: “Encontrar un camino que recorriera las 4 zonas de la ciudad pasando una sola vez por los 7 puentes y volviendo al punto de partida”. Los puentes están dibujados en azul y las zonas en rosa.
Los puentes de Königsberg: “Encontrar un camino que recorriera las 4 zonas de la ciudad pasando una sola vez por los 7 puentes y volviendo al punto de partida”. Los puentes están dibujados en azul y las zonas en rosa.
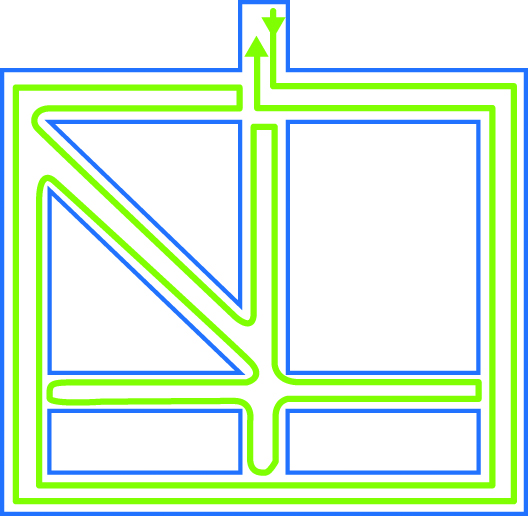 Representación del algoritmo de Thémaux.
Representación del algoritmo de Thémaux.




























