El juego de Sim, perteneciente a la familia de juegos con “lapiz y papel”, es un sencillo juego que encierra una gran riqueza matemática. Fue inventado por el matemático estadounidense, experto en criptografía, Gustavus J. Simmons, mientras trabajaba en su tesis doctoral en teoría de grafos, e inspirado en el estudio matemático de los números de Ramsey. El juego aparece en su artículo On the game of Sim (Journal of Recreational Mathematics, 1969).
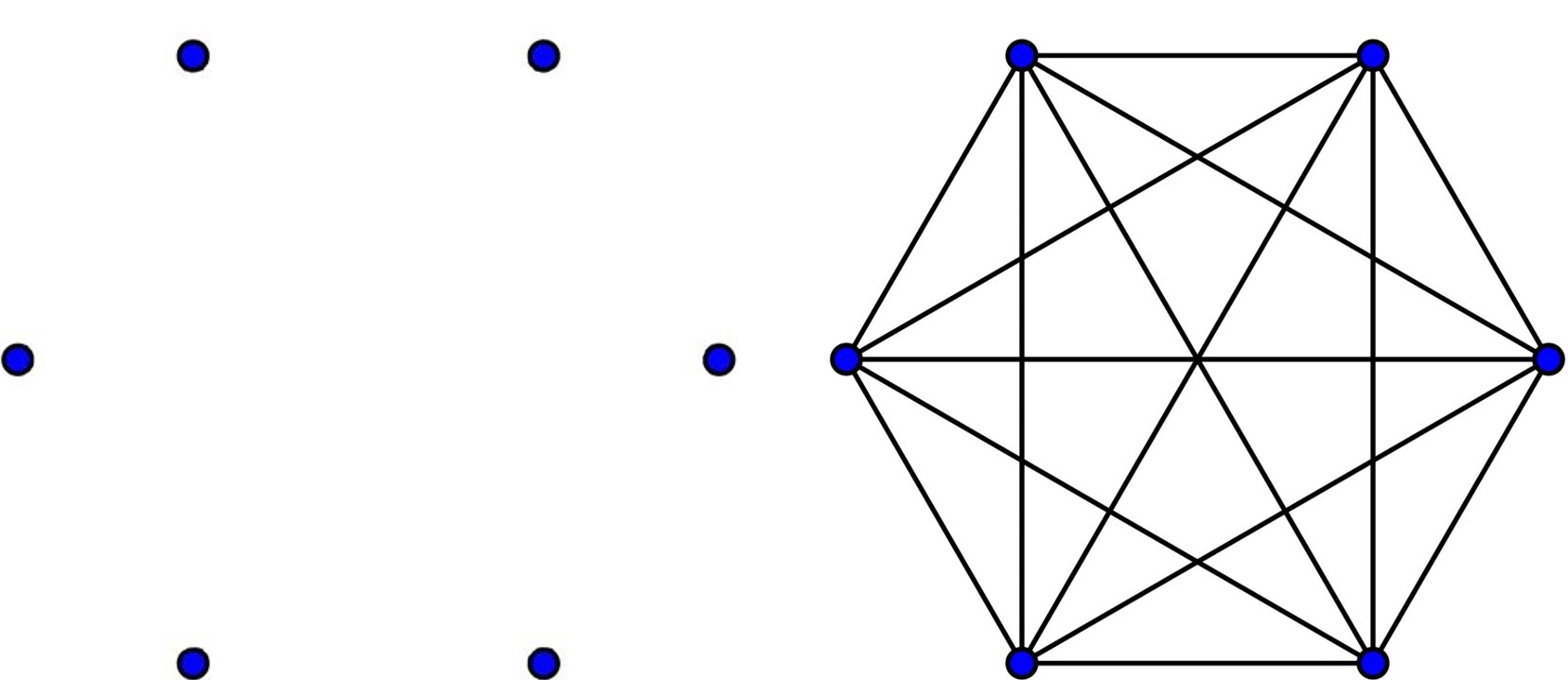
Situación inicial del juego de Sim, con los seis vértices del hexágono, y el grafo completo de seis vértices asociado K6, con los 15 posibles segmentos que unen los 6 puntos dos a dos).
Las reglas del juego son las siguientes. Se consideran los seis puntos que determinan los vértices de un hexágono regular, pintados sobre una hoja de papel. Hay 15 formas distintas de pintar un segmento que una dos vértices de la figura (como se ve en la imagen anterior), que en conjunto forman lo que se llama el grafo completo de seis puntos, K6. El juego de Sim es un juego para dos jugadores, cada uno de los cuales utiliza un lápiz de un color (por ejemplo, azul y rojo) para pintar, por turnos, un segmento que une dos puntos cualesquiera de la figura. Pierde el jugador que primero forme un triángulo monocolor, del color de su lápiz, siendo sus vértices puntos de la figura inicial.
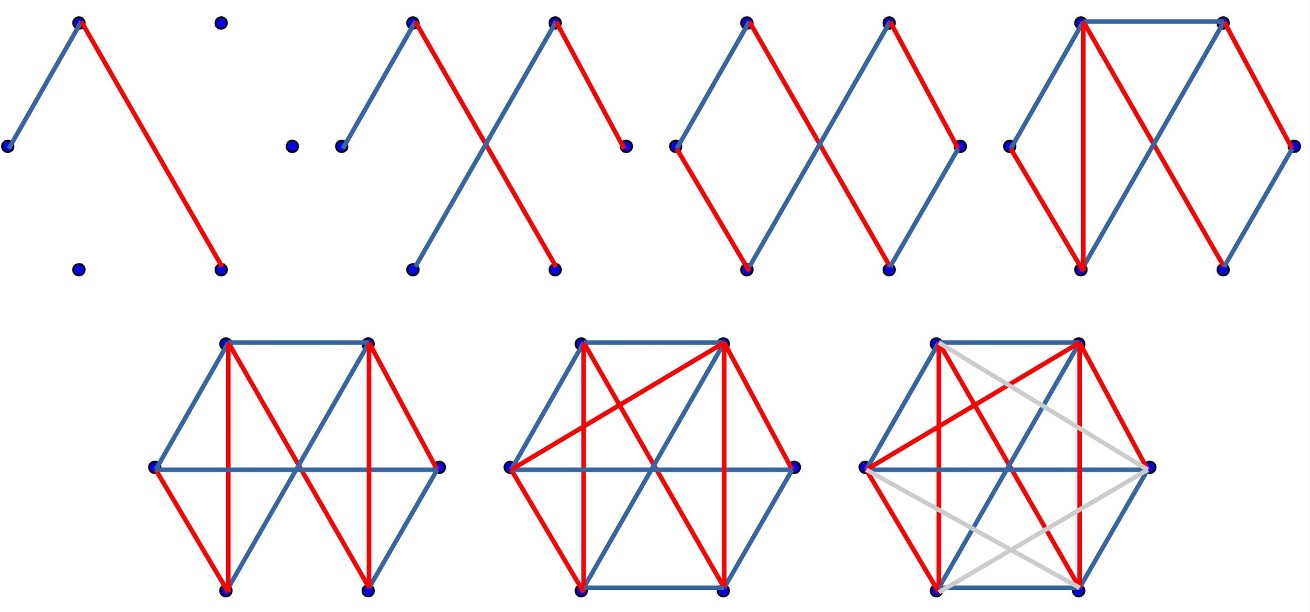
Simulación de una partida en la que el primer jugador pinta con el color azul y el segundo con el rojo. En cada instantánea se observan los dos movimientos de cada turno de ambos jugadores. Pierde el primer jugador, puesto que en el séptimo movimiento, indistintamente del segmento que pinte –en gris en la imagen- formará un triángulo azul con tres vértices del hexágono).
Una característica interesante del juego de Sim es que no puede terminar en tablas, como demostró el propio Simmons en su artículo. La demostración es la siguiente. Consideremos el grafo completo de seis puntos K6 completamente coloreado con los dos colores, es decir, los dos jugadores han continuado pintando segmentos de forma alternada hasta completar el grafo. Tomemos un vértice cualquiera v0. Como hay cinco líneas que pueden unir ese vértice del hexágono con los otros cinco (v1, v2, v3, v4, v5 en la siguiente imagen), como solamente disponemos de dos colores para pintar, al menos tres de ellas son del mismo color, por ejemplo, azul.
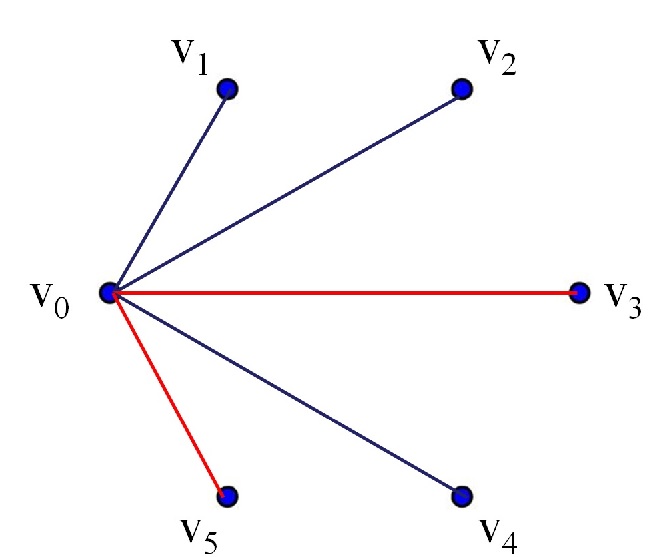
Si alguno de los tres segmentos que unen los vértices finales de esos tres segmentos azules, fuese también azul, entonces formaría un triángulo azul con los correspondientes segmentos azules que empiezan en el vértice v0. Pero si, por el contrario, ninguno de esos tres segmentos es azul, entonces los tres son rojos y forman un triángulo rojo. Por lo tanto, siempre existe un triángulo monocolor, ya sea azul o rojo. Lo cual completa la demostración.
Como consecuencia del anterior razonamiento, no existe la posibilidad de empate en el juego del Sim y alguno de los dos jugadores ganará. Sin embargo, el problema de quien de los dos jugadores tiene una estrategia ganadora y cuál es esta, es bastante complejo. De hecho, Simmons no lo incluía en su artículo, y solo después de un exhaustivo análisis con ordenadores descubrió que es el segundo jugador quien tiene una estrategia ganadora, aun así, esta no es fácil de llevar a la práctica, como ocurre con otras estrategias ganadoras que han ido descubriendo los matemáticos.
La idea que subyace al juego del Sim se enmarca dentro de la Teoría de Ramsey, esa teoría matemática del campo de la combinatoria que viene a decirnos que el desorden completo es imposible, y más concretamente está relacionada con los números de Ramsey.
La entrada El juego de Sim se publicó primero en Aprender a pensar.

