¿Què és ciència? Coneixement tan objectiu, intel·ligible i dialèctic com sigui possible. ¿I art? Coneixement, no necessàriament objectiu, intel·ligible ni dialèctic, però capaç de saltar d'una ment a una altra. Ciència i art es troben a vegades de front, a vegades de costat, a vegades l'una trepitjant els talons de l'altre, a vegades orbitant l'altre al voltant de l'una. Curiosament, les opinions sobre quina és la bona relació entre tots dos es polaritzen a prop de dos extrems. En un hi ha els que pensen que art i ciència no tenen res a veure, en l'altre els que insisteixen que art i ciència són la mateixa cosa. El primer límit no porta directament a res, i l'altre, tard o d'hora, a l'absurd.No obstant, qualsevol situació intermèdia té el seu interès. Els conceptes nuclears compartits per l'art i la ciència són dos: la intuïció i la comprensió. ¿Què és comprendre? Comprendre té a veure amb explorar el que és comú entre el que és diferent. ¿I què és intuir? Intuir és una delicada fricció entre el que ja és comprès (o observat) i el que encara està per comprendre (o per observar). El Quixot intueix, Sancho comprèn. Amb aquestes dues idees s'assagen dues afirmacions:
La grandesa de la ciència està en el fet que pot comprendre sense necessitat d'intuir (u). En efecte, la ciència s'alimenta de la percepció del món, però té un problema a l'hora d'intuir aquella part de la realitat que no pot percebre directament amb els seus sentits. És quan la realitat és invisible per massa petita, per massa gran, per massa ràpida, per massa lenta, per massa opaca, per massa transparent... Amb la mà al cor: ningú intueix la física quàntica perquè no existeixen observadors quàntics. No obstant, sí que podem comprendre la realitat amb ajuda de la quàntica. Per una altra banda: la grandesa de l'art està en el fet que pot intuir sense necessitat de comprendre (dos). D'aquí sorgeix una proposta perquè art i ciència es fecundin mútuament. Es tracta que cada una es recolzi en la seva pròpia grandesa per engrandir l'altra: l'artista serveix intuïcions científiques al científic i el científic obsequia comprensions artístiques a l'artista. ¿Això és possible? Ho és i Salvador Dalí n'és la prova. (El centre Pompidou de París recorda amb nostàlgia el clam ciutadà de l'exposició sobre Dalí el 1979 i intenta reeditar-lo el 2013.)
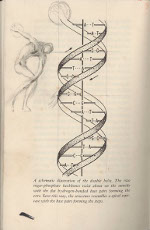
Dalí s'alimentava de ciència. Existeixen imatges d'un Dalí joveníssim amb revistes científiques sota el braç i de les seves converses amb científics com James Watson (estructura de l'ADN), Sigmund Freud (psicoanàlisi), René Thom (catàstrofes), o Ilya Prigogine (complexitat). A la tauleta del seu llit de mort van quedar textos de físics com Erwin Schrödinger, Werner Heisemberg o Albert Einstein. L'obra de Dalí està impregnada del pensament de tots aquests autors, sí, però la bona pregunta és una altra: ¿Dalí va tenir intuïcions útils per a la ciència o la matemàtica? En va tenir unes quantes. N'esmento només una.
El problema més antic de la pintura consisteix en la representació d'un volum de tres dimensions (la realitat) en una superfície de dues (el llenç). Els artistes d'Altamira ja ho van intuir fa més de 13 mil·lennis (per això utilitzaven les protuberàncies de la roca per fer-les coincidir amb les gepes dels bisons). Però 10 mil·lennis després (¡!) els cronistes murals de Mesopotàmia estaven igual: tot de perfil i en un mateix pla. Giotto intueix la perspectiva geomètrica al final de l'edat mitjana, però no arriba a comprendre-la (les línies de fuga no convergeixen). El problema no troba solució definitiva fins al Renaixement i culmina amb Las Meninas de Velázquez. Segons Michel Foucault en el pròleg del seu llibre Les Mots et les Choses, aquesta pintura introdueix a més a més el temps com a quarta dimensió. És, si es vol, l'espai de Minkowsky de la relativitat d'Einstein: tres dimensions espacials i una de temporal (¡el cine!).
Dalí s'interessa pel 3D de les holografies i de l'estereoscòpia, però no triga a intuir la seva escassa transcendència científica o filosòfica. Els científics manipulen sense problemes espais de moltes dimensions. Els comprenen però no els intueixen.
El cervell és incapaç d'imaginar-se un espai d'una dimensió superior a la del món en què viu. La proesa intel·lectual no consisteix llavors a intuir l'espai 3D sinó el 4D. La seva creu hipercúbica conté la pista genial que va seguir 20 anys després el matemàtic Thomas Banchoff per intuir allò que, fins llavors, només podia comprendre.
«¿D'on ha tret aquesta idea, mestre?», li vaig preguntar el novembre del 1985. «¡Ramon Llull! ¡Juan de Herrera!», va deixar anar sense immutar-se. O sigui: Dalí s'alimenta de De Nova Geometria del místic medieval i del Discurso sobre la figura cúbica de l'arquitecte d'El Escorial. Després pensa, conversa, somia... i engendra una nova intuïció.
Jorge Wagensberg, Dalí o la quarta dimensió, el Periódico.cat, 09/02/2013