[https:]]
 Professors (50 sin leer)
Professors (50 sin leer)






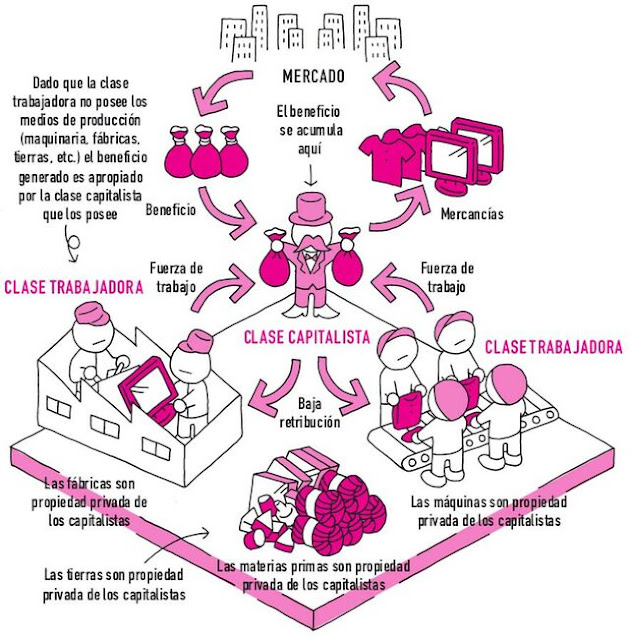
 Alguien dijo que la política consiste en una combinación de burocracia y publicidad. Burocracia para administrar el orden imperante, y publicidad para convencernos de su legitimidad. Esto siempre ha sido así. Pero si el escenario y el lenguaje con que el poder “vendía” tradicionalmente su producto eran los de la sublimidad estético-religiosa, ahora ese escenario y lenguaje son los mismos con que se publicitan el resto de mercancías (un líder o medida política se venden hoy igual que cualquier otro producto en el mercado). Ahora bien, esta secularización democrático-liberal de la propaganda política tiene sus propios problemas: el universo publicitario se expande a tal velocidad que la lucha por captar la atención (no menos dispersa) del cliente/ciudadano exige nuevos recursos. Y uno de ellos es el de la crispación. Sobre esto trata nuestra última colaboración en El Periódico Extremadura
Alguien dijo que la política consiste en una combinación de burocracia y publicidad. Burocracia para administrar el orden imperante, y publicidad para convencernos de su legitimidad. Esto siempre ha sido así. Pero si el escenario y el lenguaje con que el poder “vendía” tradicionalmente su producto eran los de la sublimidad estético-religiosa, ahora ese escenario y lenguaje son los mismos con que se publicitan el resto de mercancías (un líder o medida política se venden hoy igual que cualquier otro producto en el mercado). Ahora bien, esta secularización democrático-liberal de la propaganda política tiene sus propios problemas: el universo publicitario se expande a tal velocidad que la lucha por captar la atención (no menos dispersa) del cliente/ciudadano exige nuevos recursos. Y uno de ellos es el de la crispación. Sobre esto trata nuestra última colaboración en El Periódico Extremadura




Arte e invierno casan bien. Una buena propuesta para estos fríos días invernales es acercarse a las exposiciones de arte. Y si es con los pequeños y pequeñas de la casa (y quienes no lo son tanto), mejor. Es una interesante oportunidad para conocer las creaciones artísticas y acercar el arte a toda la familia… o a nuestro alumnado, si somos docentes. Y una cosa muy recomendable es comenzar con algunas de las exposiciones de pintoras.
El mundo del arte, tal y como nos lo enseñan, se nos muestra como un ámbito restringido a los varones, donde las artistas no están presentes. De hecho, solo tenemos que preguntarnos a nosotros mismos a qué pintoras conocemos y, en general y salvo excepciones, conocemos o pocas o incluso ninguna. Claro, lo siguiente es pensar que ellas no han podido crear, no tienen obra y por esta razón no las conocemos. Es decir, que no hay. Y ahí ya tenemos el error de percepción instalado como una certeza: no hay casi pintoras. Un error que, desgraciadamente y en forma de prejuicio, nos amputa buena parte de nuestro legado artístico. Un legado que nos pertenece a todos, mujeres y hombres.
Esta falsa impresión viene dada por el silenciamiento y la falta de divulgación de toda la creación artística de autoría femenina… que, además, nos produce una idea de arte claramente empobrecida, carencial, pues de ella hemos expulsado toda la obra que desde siempre han creado las artistas y nos hemos quedado tan tranquilos.
No está de más recordar que la producción de las pintoras (y las músicas y las escritoras y las científicas) se ha visto mediatizada por unas barreras sociales mucho mayores —como su menor acceso a la educación y la cultura— que les impedían desarrollar una carrera fuera del ámbito del hogar. Esto se ha visto reflejado en la elección de géneros —como el bodegón, las flores o los retratos— que han sabido tratar con maestría o con perspectivas, formatos y temáticas diferentes. Ellas aportan un punto de vista y una maestría sin la cual no está completa nuestra tradición artística.
Sin embargo, la sistemática ausencia de los museos, las exposiciones, las historias del arte o los manuales han “normalizado” una cultura, un arte, cuyos únicos protagonistas son los hombres, un arte que parece posible sin mujeres. Un despropósito, vamos. Una carencia importante para nuestra visión de mundo, que se va forjando sin ellas.
Por eso, visitar las exposiciones de pintoras resulta algo especialmente recomendable. Sobre todo, para los más pequeños de la casa, para quienes el mundo del arte se abre de una forma incomparablemente más rica, pues normalizan desde el principio el arte como un espacio creado por artistas hombres y mujeres… pero también —y eso, además, a las niñas les viene muy bien— les presenta modelos de ser mujer. La verdad es que a ellas les da mucha seguridad, se ven dueñas de sí, capaces de poder elegir cualquier opción en la vida porque, efectivamente, tienen modelos. Eso de “yo, de mayor, quiero ser como…”
Este invierno en Madrid nos encontramos con algunas exposiciones estupendas que pueden servirnos para acercarnos a algunas de las mejores pintoras.
La primera la presenta El Prado. Una estupenda exposición de dos de las más relevantes pintoras del XVI: Sofonisba Anguissola y Lavinia Fontana.
 Autorretrato en el caballete, Sofonisba Anguissola. «1001 Pinturas que debes ver antes de morir». Muzeum Zamek w Lancucie, Lancut,
Autorretrato en el caballete, Sofonisba Anguissola. «1001 Pinturas que debes ver antes de morir». Muzeum Zamek w Lancucie, Lancut,
Sofonisba Anguissola brilló en la corte de Felipe II como pintora, lo que le dio una repercusión y un notable reconocimiento en la época. Nació en una familia italiana que educó muy bien a sus hijas, una de sus hermanas, Lucía, también destacó en la pintura. Sus cuidados y vivos retratos están entre lo mejor de su estupenda producción y transmiten con gran delicadeza valores ligados al humanismo y al saber, así como a la familia. Entre los retratos de Sofonisba encontramos el muy conocido de Felipe II, casi su retrato oficial, que había sido atribuido a otros pintores hasta que se reconoció su autoría. O el retrato de la poderosa e intrigante, además de bella y tuerta, Princesa de Éboli, con esa determinación, distancia y delicadeza que imprime a su mirada y a su talante.
 Retrato de un prelado California, 1580. Atribuido a Lavinia Fontana.
Retrato de un prelado California, 1580. Atribuido a Lavinia Fontana.Por su parte, Lavinia Fontana nació en Bolonia en un siglo que vio tantas grandes pintoras, como Barbara Longhi, Elisabetta Sirani o la gran Fede Galizia, pionera de los bodegones y cuya excelencia marcó la composición y el canon del género. Lavinia tuvo una exitosa carrera, donde llegó a disputar y obtener encargos papales. Jugaba en primera liga. Su marido siempre reconoció el talento de Lavinia y actúo como colaborador y ayudante de su esposa, sin que se le cayeran los anillos, lo que le valió recibir críticas en su tiempo. Pero parece que fue una pareja muy bien avenida, con once hijos y una buena colaboración en el trabajo. Como vemos, todas las épocas tienen hombres auténticos que no se dejan llevar por prejuicios.
Esta es la segunda exposición sobre pintoras que hacen en El Prado en más de 200 años. Así que ya les vale. Sobre todo, porque existen muy pocas posibilidades de poder ver esa brillante e indispensable producción artística y eso es cometido del museo divulgarla y darla a conocer. Parece que las cosas van cambiando y vamos notando la necesidad de conocer a nuestras artistas también. Menos mal.
 «Mamá», de Louis Bourgeois
«Mamá», de Louis Bourgeois
Pero no solo está el Prado, también el Reina Sofía presenta exposiciones y colecciones muy interesantes. Encontramos las monográficas individuales, como la de Louise Bourgeois —Louise Bourgeois. El cuerpo en exilio (1947-49)— o la hispano-brasileña Sara Ramo —lindalocaviejabruja— , entre otras muy interesantes, y las colectivas como la de las artistas pop —Fuera del canon. Las artistas pop en España— o de las artistas que compartieron reivindicaciones —Vindicaciones feministas—. Todas ellas nos permiten conocer parte de la obra de estas artistas, algo estupendo. Pero todavía mejor es el planteamiento de algunas de estas exposiciones, que (¡por fin!) ya integran a pintoras cuando ofrecen las obras de una corriente. Ese planteamiento es el que permite ir resituando los referentes, entretejiendo memoria.
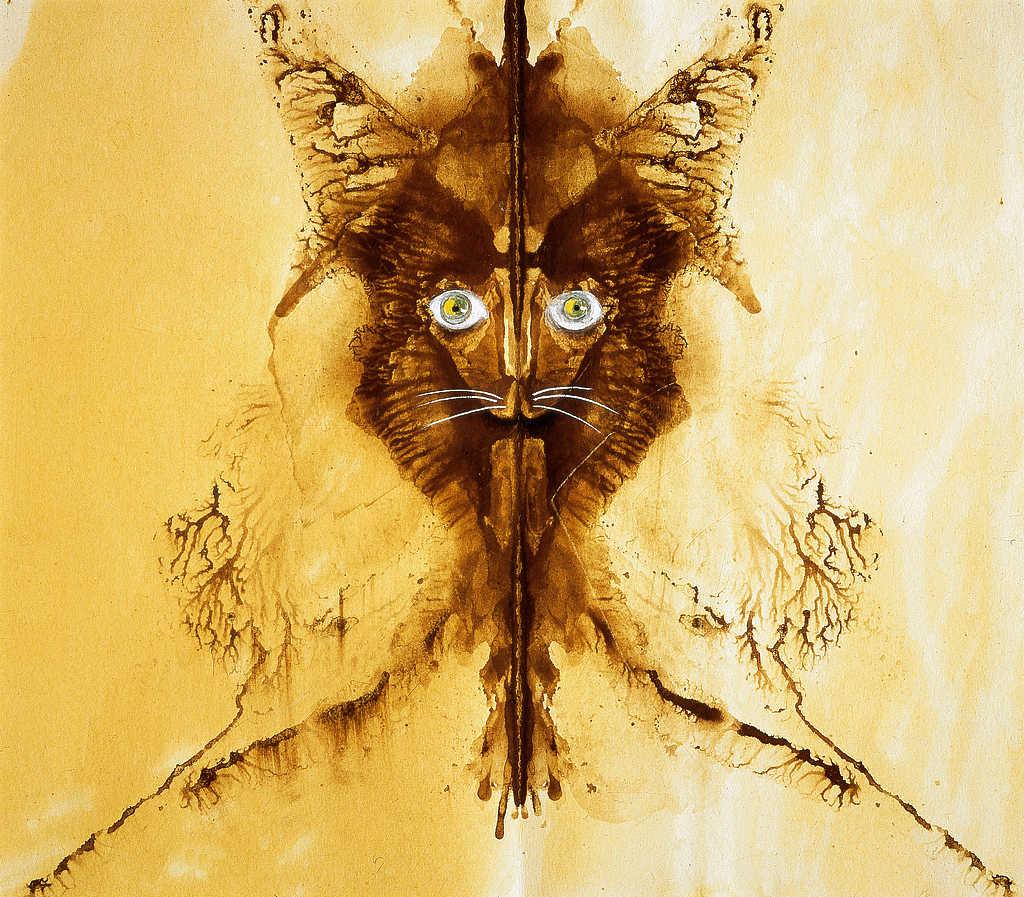 «El hombre gato», de Remedios Varo.
«El hombre gato», de Remedios Varo.Es lo que ocurre cuando presentan el surrealismo (El surrealismo en el exilio español) y no se olvidan ya de Remedios Varo
 «Mujer con guitarra», de María Blanchard.
«Mujer con guitarra», de María Blanchard.
o el cubismo (Cubismo y modernidad) y no olvidan tampoco de María Blanchard. Algo que era y sigue siendo muy habitual. Falta más, pero ese es el camino. El hecho de tenerlas presentes en el tejido de la época las incorpora a la memoria colectiva y, así, va ampliando nuestro entramado cultural, hasta ahora habitado casi exclusivamente por hombres, con las creaciones de ellas. Resultan imprescindibles para saber cómo y qué se creó desde ese otro espacio de la sociedad habitado por mujeres sobre el que no solemos fijar la mirada.
Por todo ello, es muy recomendable acercarse a dar una vuelta por allí y comentar las cosas que nos gustan y nos sorprenden o extrañan. Cualquiera de estas propuestas u otras –en el Reina Sofía hay bastantes más— nos pueden servir. Con las pequeñas y los pequeños de la casa o la escuela, sobre todo. Así vamos creando, de verdad, un conocimiento individual que va tramando una cultura compartida, más real, donde todas las personas, mujeres y hombres, se ven reconocidas en las creaciones. En definitiva, una cultura universal, no restringidamente masculina, más amplia, matizada y diversa que nos enriquece a todas. Ese es el tema.

Ana López Navajas es profesora de Lengua y Literatura, investigadora vinculada a la Universitat de València y asesora de Coeducación e Igualdad en la Formación del Profesorado en la Conselleria.
La entrada El arte de las pintoras se publicó primero en Aprender a pensar.




















Raúl Ibáñez, profesor de Geometría y Topología de la UPV.
En 1924, el pintor futurista italiano Giacomo Balla (1871-1958) creó una obra titulada Los números enamorados asociando una cualidad humana, como es el enamoramiento, a los números. También en el ámbito de las matemáticas nos gusta asociar a los números, en particular, a los números naturales, cualidades humanas. Existen números amigos, sociables, novios, narcisistas, felices, tristes, hambrientos, intocables, ambiciosos, afortunados, malvados, odiosos, prácticos o raros, pero también con otras denominaciones curiosas, como números vampiros, parásitos, perniciosos, apocalípticos, perfectos, sublimes, abundantes, escasos o intocables.
Algunas de estas familias de números deben su propiedad definitoria al comportamiento de sus divisores propios, es decir, entre los divisores no se considera al propio número. Así, un número se dice que es perfecto si es igual a la suma de sus divisores, como el 6 = 1 + 2 + 3 o el 28 = 1 + 2 + 4 + 7 + 14.
Mientras que los números que no son perfectos pueden ser abundantes, cuando el número es menor que la suma se los divisores, como el 12 < 1 + 2 + 3 + 4 + 6 = 16, o deficientes en el caso contrario, como el 14 > 1 + 2 + 7 = 10 o todos los números primos.
Un número es ambicioso si puede llegar a ser perfecto de la siguiente forma, dado el número se toma la suma de sus divisores, con este nuevo número se vuelve a considerar la suma de sus divisores, y se continúa así, de forma que el número es ambicioso si llega un momento que se alcanza un número perfecto, como en el caso del número 95, cuyos divisores suman 1 + 5 + 19 = 25, y los divisores de este suman 1 + 5 = 6, que es perfecto, aunque el 24 o los números primos no son ambiciosos.
Relacionados con la perfección están los números sublimes, aquellos tales que el número de sus divisores (incluido el propio número) y la suma de los mismos son perfectos, como el 12, que tiene 6 divisores y su suma es 1 + 2 + 3 + 4 + 6 + 12 = 28, aunque solo se conoce otro número sublime más, que es
6086555670238378989670371734243169622657830773351885970528324860512791691264.
Se dice que dos números son amigos si cada uno de ellos es igual a la suma de los divisores del otro. Un ejemplo son los números 220 = 1 + 2 + 4 + 71 + 142 y 284 = 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110, que fueron utilizados en la antigüedad para realizar talismanes relacionados con la amistad y el amor, por lo que quizá estos deberían ser llamados números enamorados. Y dos números se consideran novios o casi-amigos si cada uno de ellos es igual a la suma de sus divisores menos 1, como el 48 = 1 + 3 + 5 + 15 + 25 – 1 y el 75 = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 – 1.
La propiedad de amistad puede generalizarse a un grupo de números, de forma que la suma de los divisores de cada uno es igual al siguiente, y la del último igual al primero, entonces se habla de números sociables. El grupo de números más pequeños que son sociables son 12.496, 14.288, 15.472, 14.536 y 14.264.
También existen intocables dentro de la familia de los números naturales, son aquellos que no se pueden expresar como suma de los divisores de ningún número. El número 2 es intocable, el 3 no (1 + 2, divisores del 4), el 5 no (1 + 3, divisores del 9) y el 5 sí, ya que solo puede expresarse como 1 + 4, pero si el 4 es divisor del número, también lo es el 2 y la suma sería al menos 7, y el siguiente intocable es el 52.
Y no podían faltar los números raros, que son aquellos que son abundantes, es decir, la suma de los divisores es mayor que el número, pero no se puede obtener el número exacto quitando algunos de los divisores, es decir, como suma de un subconjunto de divisores propios. Por ejemplo, el 12 es abundante, pero como 12 = 2 + 4 + 6, no es raro, y el número raro más pequeño es 70 (cuyos divisores son 1, 2, 5, 7, 10, 14, 35).
Cerramos este repaso a algunas tribus numéricas con los números poderosos, que son aquellos tales que, si un número primo p es divisor suyo, también lo es su cuadrado p2, como el 36, cuyos divisores primos son 2 y 3, y sus cuadrados también son divisores de 36.
Puede resultar atractivo para los alumnos trabajar en el aula estos grupos de números creando un juego que consista en buscar números pertenecientes a las diferentes familias mencionadas aquí.
La entrada Los números enamorados se publicó primero en Aprender a pensar.

Ana Casado, editora de SM.
Los laberintos han llamado la atención desde tiempos inmemoriales. Son muy conocidos el laberinto mitológico de Dédalo, en Creta, al que accedió Teseo para derrotar al Minotauro y regresar con ayuda del ovillo que le entregó Ariadna; y el laberinto egipcio de las tres mil estancias del faraón Amenemhet.
A partir del siglo XVIII, en Europa crece el interés y se construyen jardines-laberintos como lugares lúdicos: Hampton Court, en Inglaterra, Villa Alteri, en Roma, el laberinto de Horta en Barcelona…
Este verano descubrí cerca de mi lugar de vacaciones el laberinto de Villapresente. También llamó la atención de mis sobrinos y nos acercamos a tratar de superar el reto. Pero, ¿cómo salir de un laberinto?
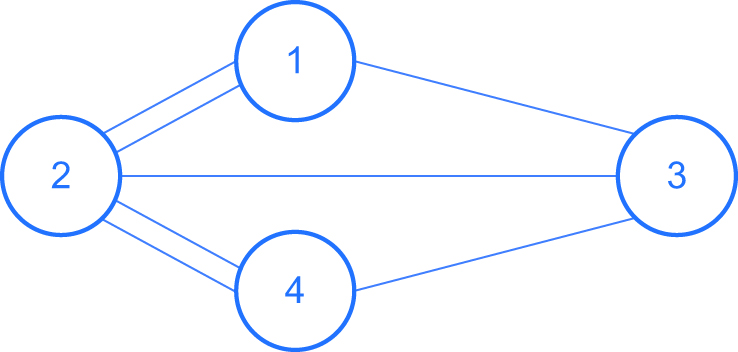
Cualquier laberinto se puede representar mediante un grafo dirigido. Un grafo es un conjunto de nodos unidos por aristas. Es dirigido si las aristas tienen un sentido.
Los caminos del laberinto corresponden a las aristas del grafo y los cruces y estancias a los nodos. Veamos un ejemplo:
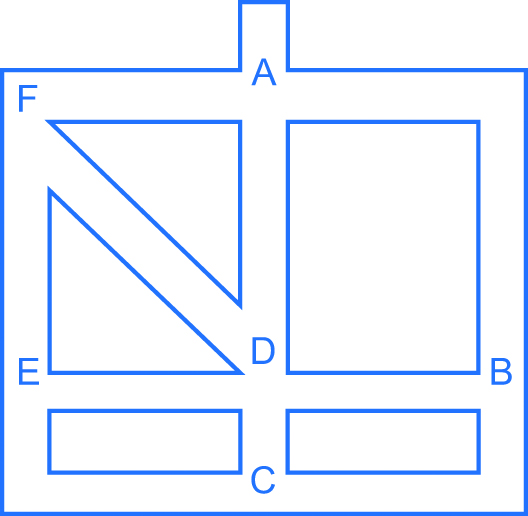 Laberinto.
Laberinto.
 Representación del laberinto como grafo.
Representación del laberinto como grafo.
El matemático Leonard Euler (1707-1783) fue el precursor de la teoría de grafos. A partir del famoso problema de los puentes de Königsberg, demostró que en un grafo, “se puede encontrar un camino que parta de un nodo inicial, recorra todos los nodos pasando una sola vez por cada arista y vuelva al nodo inicial, siempre que el grado de cada nodo sea par”. (El grado de un nodo es el número de aristas que inciden en él). Este camino se denomina circuito euleriano.
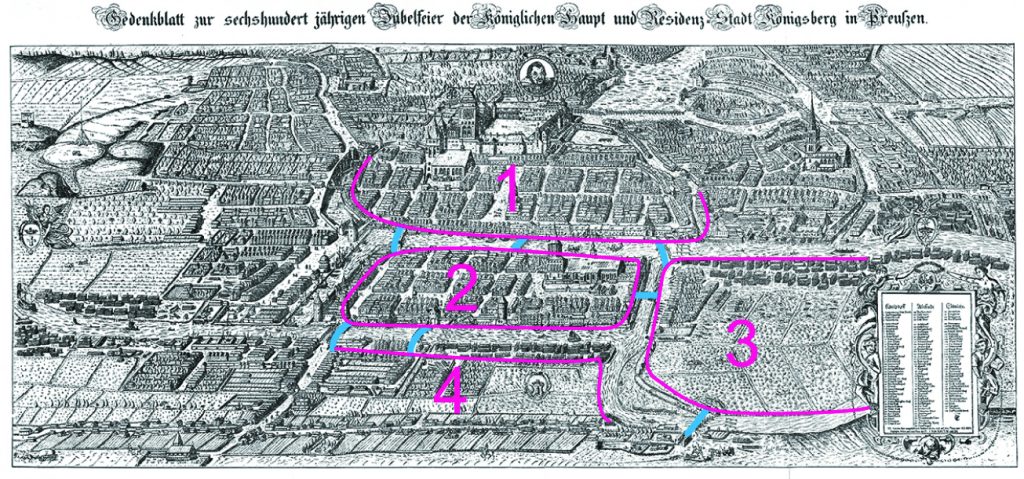 Los puentes de Königsberg: “Encontrar un camino que recorriera las 4 zonas de la ciudad pasando una sola vez por los 7 puentes y volviendo al punto de partida”. Los puentes están dibujados en azul y las zonas en rosa.
Los puentes de Königsberg: “Encontrar un camino que recorriera las 4 zonas de la ciudad pasando una sola vez por los 7 puentes y volviendo al punto de partida”. Los puentes están dibujados en azul y las zonas en rosa.
El grafo correspondiente es:
Como se puede ver todos los nodos son de grado impar por lo que no existe un camino con las condiciones pedidas.
En el caso de grafos dirigidos, la condición para que exista un circuito euleriano es que “el número de aristas que llegan a un nodo coincida con el número de aristas que salgan de él”.
Por tanto, en un laberinto siempre vamos a encontrar un circuito euleriano, un camino que pase por todos los cruces o estancias y recorra una sola vez cada arista. En algún punto del recorrido hallaremos la salida.
Muchos autores han buscado procedimientos para recorrer los laberintos de forma ordenada. El matemático francés Edouard Lucas (1842-1891) recoge en su libro Récréations Mathématiques el algoritmo Trémeaux propuesto por el ingeniero Charles Trémeaux. Es considerado, actualmente, el más eficiente. Los pasos son los siguientes:
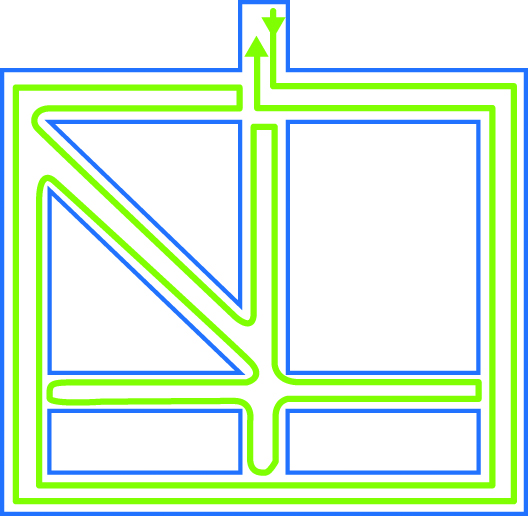 Representación del algoritmo de Thémaux.
Representación del algoritmo de Thémaux.
Este algoritmo permite recorrer un laberinto desde el punto inicial o desde cualquier punto interior en el que nos encontremos. No será el camino más corto, pero sí hallaremos la salida.
Este método general permite recorrer cualquier laberinto. Si el laberinto se puede representar como un árbol conexo, es decir, un grafo en el que dos nodos cualesquiera están conectados por exactamente un camino, podremos salir del laberinto usando un método más sencillo:
Elegimos uno de los lados (izquierdo o derecho) de los muros o setos que limitan el camino y recorreremos el laberinto sin despegar la mano del muro hasta encontrar la salida.
La entrada ¿Cómo salir de un laberinto? se publicó primero en Aprender a pensar.






















Grupo de Historia de las Matemáticas de la RSME.
Durante varios siglos, Europa ha tenido una posición hegemónica en las ciencias y las matemáticas universales, lo que no debe hacer olvidar ni las raíces orientales de la matemática europea, las anteriores a la Grecia clásica, primero, y las previas al Renacimiento, después, ni la existencia de una matemática autóctona en cualquier cultura florecida antes de su contacto con la occidental o europea.
Pero no todas la naciones europeas contribuían en igual medida a esa hegemonía. En A concise history of mathematics, Dirk J. Struik, matemático e historiador de la matemática holandés nacionalizado norteamericano, escribió (1948): “Cuando se inició el siglo veinte, la matemática se encontraba floreciente, aunque la matemática creativa estaba todavía confinada en una parte del mundo, era en muchos casos una profesión académica y restringida, con algunas excepciones, a los varones de la estirpe europea. Los países líderes seguían siendo Francia y Alemania”.
En este entorno de 1900, la situación de España no era floreciente sino periférica, lo que significa ser un país receptor neto de la ciencia creada en otros lugares de la comunidad científica internacional.
Al escribir “todavía”, Struik era consciente de que la situación estaba cambiado con el transcurso del siglo XX; en efecto, otros países no europeos se iban incorporando a ese florecimiento, se han incorporado de hecho incluso tomando posiciones adelantadas. También la restricción de género en la creatividad matemática se está liberando, en un proceso que tiene aún camino por recorrer.
La posición matemática periférica de España se ha difuminado notablemente a lo largo del siglo XX, teniendo un momento brillante en el tramo final de la Edad de Plata de la Cultura Española, que quedó aniquilada por la Guerra Civil y la posterior represión. La aproximación de la matemática española a la matemática internacional floreciente resurgió con auge al tiempo que la España democrática pasaba en 1985 a formar parte de las Comunidades Europeas, que pasaron a ser la Unión Europea (UE) en 1993.
Entre las numerosas iniciativas que se pusieron en marcha en la UE para promover una nueva identidad europea reforzada, surgió la obra colectiva L’Europe mathématique: histoire, mythes, identités (Ed. La Maison des Sciences de l´’Home, 1996). Uno de sus capítulos, escrito por el matemático e historiador de la matemática argentino Eduardo L. Ortiz, está dedicado a la conexión de la comunidad matemática internacional durante el siglo XIX con la “periferia ibérica”, que en Europa forman España y Portugal, y al otro lado del Atlántico, América Latina.
Este artículo sirve de coartada para destacar los paralelismos y las coincidencias a lo largo de la historia de las matemáticas en España y Portugal, afirmando la conveniencia de que ambas se consideren de modo conjunto, no solo en el período contemporáneo sino a lo largo de toda la historia, incluyendo las dominaciones romana y árabe y, por supuesto, los momentos estelares en los inicios de la navegación oceánica.
Desde el Grupo de Historia de las Matemáticas de la RSME (GHM/RSME) y el Seminário Nacional de História da Matemática de la Sociedade Portuguesa de Matemática (SNHM/SPM) se vienen proponiendo “Encuentros Ibéricos de Historia de las Matemáticas” con el fin de aproximar a las comunidades de historiadores de las matemáticas de ambos países y promover el trabajo en común.
El primero tuvo lugar en Santiago de Compostela el año 2013, el segundo en Coimbra en 2016 y el tercer encuentro ha sido este año en Sevilla, del 26 al 28 de septiembre. La cita del Encuentro/Encontro de este año ha sido particularmente adecuada al coincidir con el inicio del quinto centenario de la primera circunnavegación del Globo, para el que los Gobiernos de España y Portugal han presentado un programa conjunto de acciones que serán auspiciadas por la UNESCO, declarando aquella gesta del primer cuarto del siglo XVI como Patrimonio Mundial de la Humanidad.
Quince días antes se había inaugurado en el Archivo General de Indias de Sevilla la exposición “El viaje más largo”, sobre los aspectos humanos y científicos de la aventura de los navegantes que dieron la primera vuelta al mundo. Partieron hacia alta mar desde Sanlúcar de Barrameda el 20 de septiembre de 1519, eran 239 tripulantes de varias naciones europeas repartidos en cinco barcos al mando del marino portugués Fernando de Magallanes. La larga y accidentada travesía oceánica finalizó también en Sanlúcar tres años después, cuando solo arribó la nave Victoria con 18 supervivientes capitaneados por el marino español Juan Sebastián Elcano.
En el tercer Encuentro/Encontrose se han tratado temas diversos, pero historiadores españoles y portugueses han dado cuenta de investigaciones muy relevantes sobre el papel de la experiencia, la ciencia y la matemática en la cultura náutica, incluyendo la elaboración de mapas.
La entrada Encuentros Ibéricos de Historia de las Matemáticas se publicó primero en Aprender a pensar.






