Ana Casado, editora de SM.
Los laberintos han llamado la atención desde tiempos inmemoriales. Son muy conocidos el laberinto mitológico de Dédalo, en Creta, al que accedió Teseo para derrotar al Minotauro y regresar con ayuda del ovillo que le entregó Ariadna; y el laberinto egipcio de las tres mil estancias del faraón Amenemhet.
A partir del siglo XVIII, en Europa crece el interés y se construyen jardines-laberintos como lugares lúdicos: Hampton Court, en Inglaterra, Villa Alteri, en Roma, el laberinto de Horta en Barcelona…
Este verano descubrí cerca de mi lugar de vacaciones el laberinto de Villapresente. También llamó la atención de mis sobrinos y nos acercamos a tratar de superar el reto. Pero, ¿cómo salir de un laberinto?
Cualquier laberinto se puede representar mediante un grafo dirigido. Un grafo es un conjunto de nodos unidos por aristas. Es dirigido si las aristas tienen un sentido.
Los caminos del laberinto corresponden a las aristas del grafo y los cruces y estancias a los nodos. Veamos un ejemplo:
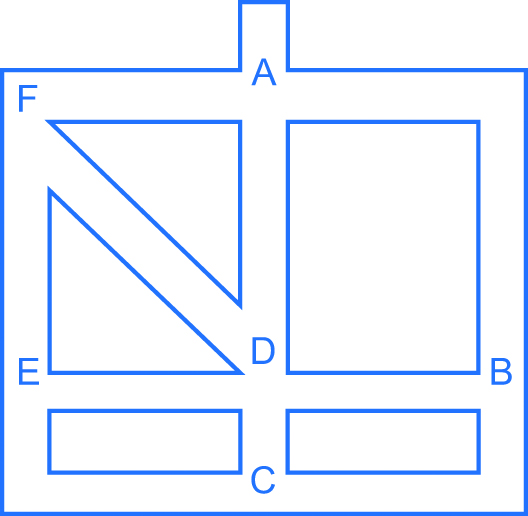 Laberinto.
Laberinto.
 Representación del laberinto como grafo.
Representación del laberinto como grafo.
El matemático Leonard Euler (1707-1783) fue el precursor de la teoría de grafos. A partir del famoso problema de los puentes de Königsberg, demostró que en un grafo, “se puede encontrar un camino que parta de un nodo inicial, recorra todos los nodos pasando una sola vez por cada arista y vuelva al nodo inicial, siempre que el grado de cada nodo sea par”. (El grado de un nodo es el número de aristas que inciden en él). Este camino se denomina circuito euleriano.
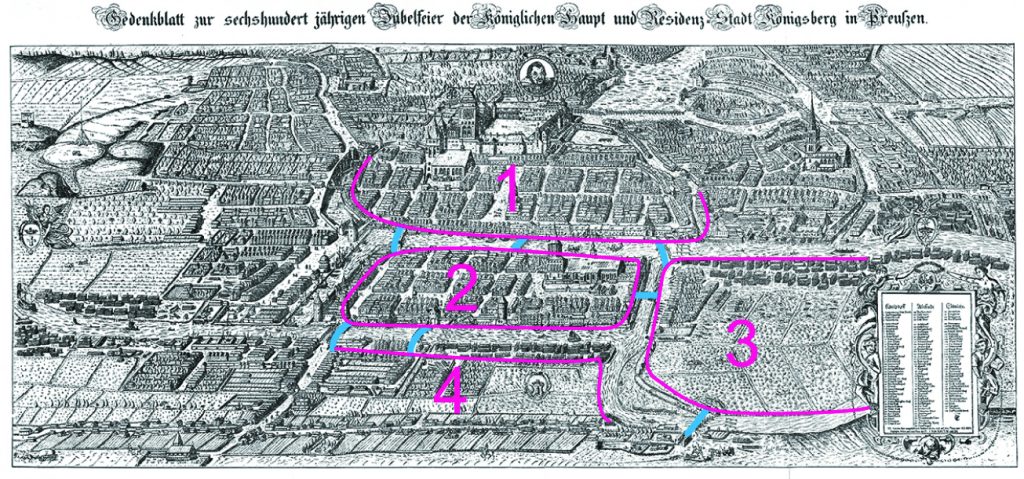 Los puentes de Königsberg: “Encontrar un camino que recorriera las 4 zonas de la ciudad pasando una sola vez por los 7 puentes y volviendo al punto de partida”. Los puentes están dibujados en azul y las zonas en rosa.
Los puentes de Königsberg: “Encontrar un camino que recorriera las 4 zonas de la ciudad pasando una sola vez por los 7 puentes y volviendo al punto de partida”. Los puentes están dibujados en azul y las zonas en rosa.
El grafo correspondiente es:
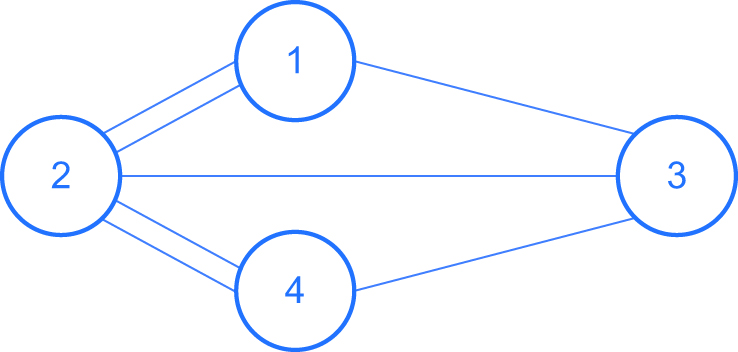
Como se puede ver todos los nodos son de grado impar por lo que no existe un camino con las condiciones pedidas.
En el caso de grafos dirigidos, la condición para que exista un circuito euleriano es que “el número de aristas que llegan a un nodo coincida con el número de aristas que salgan de él”.
Por tanto, en un laberinto siempre vamos a encontrar un circuito euleriano, un camino que pase por todos los cruces o estancias y recorra una sola vez cada arista. En algún punto del recorrido hallaremos la salida.
Muchos autores han buscado procedimientos para recorrer los laberintos de forma ordenada. El matemático francés Edouard Lucas (1842-1891) recoge en su libro Récréations Mathématiques el algoritmo Trémeaux propuesto por el ingeniero Charles Trémeaux. Es considerado, actualmente, el más eficiente. Los pasos son los siguientes:
- En el punto inicial, elegimos un camino cualquiera.
a. Si llegamos a una estancia sin salida, retrocedemos por el camino recorrido.
b. Si llegamos a un cruce, elegimos uno de los caminos aún no recorridos. Hacemos una marca en el camino que nos ha llevado a este cruce y una marca en el cruce para saber qué ya lo hemos visitado. - Si llegamos a un cruce ya visitado…
a. Por un camino distinto, recorremos este camino en sentido inverso. Hacemos dos marcas en el camino, para señalar que lo hemos recorrido en los dos sentidos.
b. Por un camino ya recorrido en los dos sentidos, elegimos un camino nuevo y si no es posible, un camino recorrido en un solo sentido.
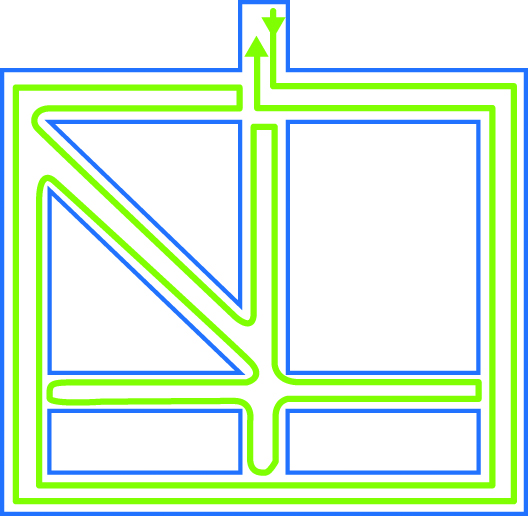 Representación del algoritmo de Thémaux.
Representación del algoritmo de Thémaux.
Este algoritmo permite recorrer un laberinto desde el punto inicial o desde cualquier punto interior en el que nos encontremos. No será el camino más corto, pero sí hallaremos la salida.
Este método general permite recorrer cualquier laberinto. Si el laberinto se puede representar como un árbol conexo, es decir, un grafo en el que dos nodos cualesquiera están conectados por exactamente un camino, podremos salir del laberinto usando un método más sencillo:
Elegimos uno de los lados (izquierdo o derecho) de los muros o setos que limitan el camino y recorreremos el laberinto sin despegar la mano del muro hasta encontrar la salida.
La entrada ¿Cómo salir de un laberinto? se publicó primero en Aprender a pensar.



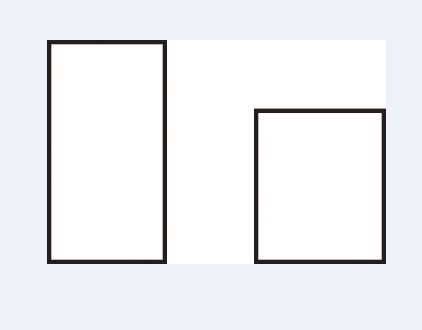
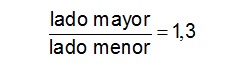
 Proporción humana y proporción divina.
Proporción humana y proporción divina.
 Portada de la Mezquita de Córdoba.
Portada de la Mezquita de Córdoba.
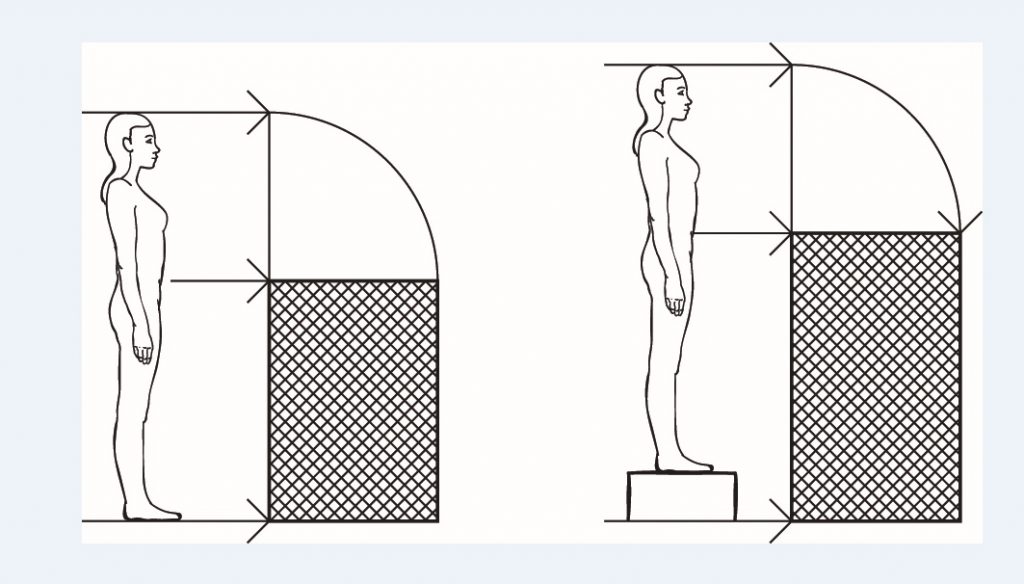
 Proporción áurea.
Proporción áurea.
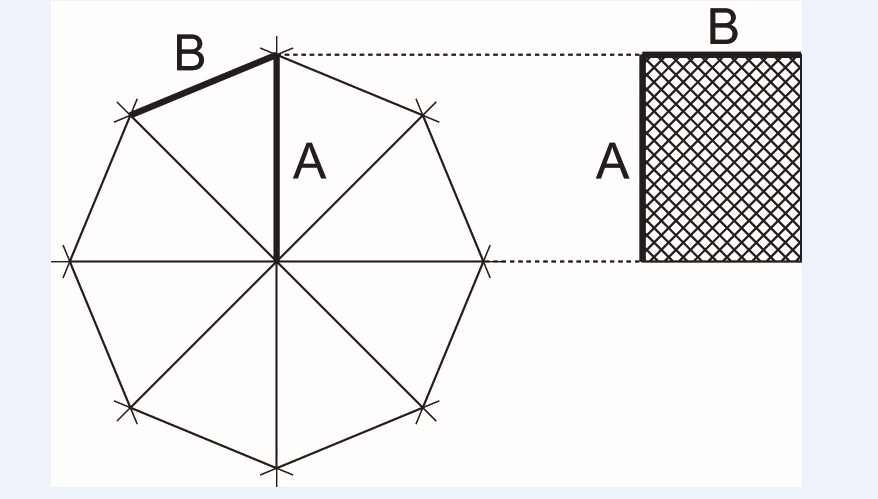 Proporción cordobesa.
Proporción cordobesa.






 Una pieza representa un caramelo.
Una pieza representa un caramelo.






 dentro. Le preguntaremos: ¿Cuántas canicas hay? Y ellos dirán: muchas. Sacaremos alguna canica de la bolsa y les volvemos a preguntar, ¿cuántas canicas hay ahora? Ellos contestarán que menos, pero todavía hay muchas. Repetiremos el proceso hasta que solo quede 1 en la bolsa y volveremos a preguntar. Contestarán: una bolsa canicas
dentro. Le preguntaremos: ¿Cuántas canicas hay? Y ellos dirán: muchas. Sacaremos alguna canica de la bolsa y les volvemos a preguntar, ¿cuántas canicas hay ahora? Ellos contestarán que menos, pero todavía hay muchas. Repetiremos el proceso hasta que solo quede 1 en la bolsa y volveremos a preguntar. Contestarán: una bolsa canicas



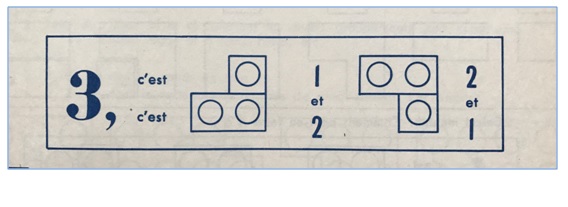


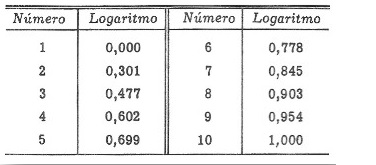

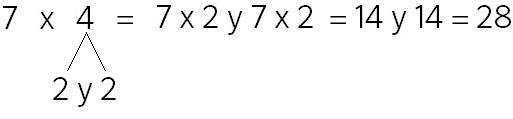
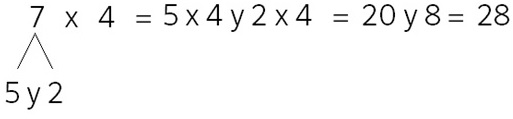
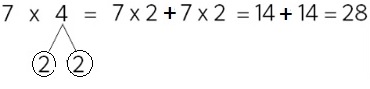
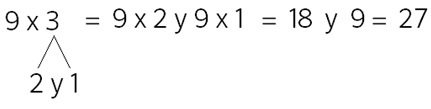
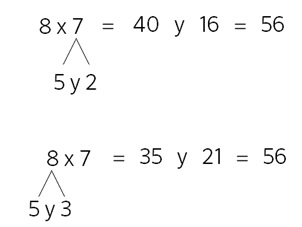
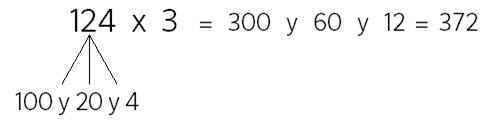

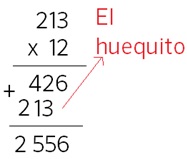
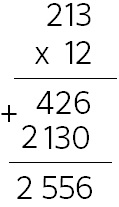
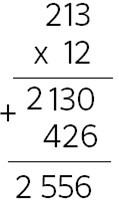



 Paso 1. Juego libre
Paso 1. Juego libre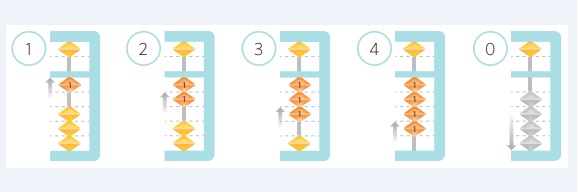
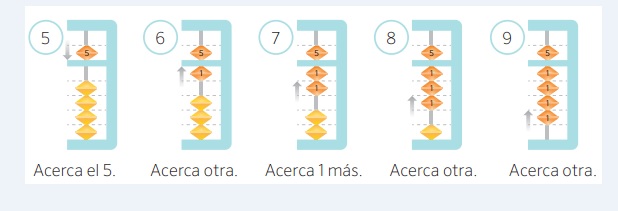
 Mira la palma de tu mano derecha. ¿Eres capaz de encontrar las piezas de valor uno? ¿Eres capaz de encontrar la pieza de valor cinco?
Mira la palma de tu mano derecha. ¿Eres capaz de encontrar las piezas de valor uno? ¿Eres capaz de encontrar la pieza de valor cinco?








 ¡Mira, un altobús!
¡Mira, un altobús! La camiseta anterior
La camiseta anterior ¡Mira, un altobús!
¡Mira, un altobús! La camiseta anterior
La camiseta anterior