BLOCS DE FILOSOFIA » marzo 14, 2018

« Expand/Collapse

(11 sin leer)

marzo 14, 2018
18:14
Ahorita
» ‎ El café de Ocata

He conocido a una mujer que conoció a la mujer más hermosa de la historia de México, que además de ser magnificentemente hermosa estaba convencida de que era la encargada de hacer salir el sol día tras día. Pero sigo sin conocer el significado de "ahorita". He comido chiles rabiosos que le dan un significado escatológico a la pimienta. Pero sigo sin entender el matiz del "ahoritita". He subido a las pirámides del sol y de la luna en Teotihuacán y he bebido mezcales dignos de los dioses. Pero "el ahorita ahorita" se me resiste. He viajado en el metro de México a hora punta en una tarde lluviosa y he acabado con medio cuerpo dormido y tortícolis y he tratado con personas cultísimas de memoria caligráfica en restaurantes de no sé cuántos tenedores. Pero el pinche ahorita de su pinche madre, me desconcierta. He visto salir el sol y la luna y niños más pequeños que mis nietos esnifando pegamentos junto a charcos grasientos en los que se reflejaba rutilante toda la tristeza del mundo y he leído el periódico que escribieron los exiliados del Sinaia camino de Veracruz. Cada día me desaparecía de la habitación del hotel un cuaderno, un lápiz, un boli y un sacapuntas y cada día los renovaba para poder seguir renovándolos. He visto enajenados por las calles con más baches bailando su inocencia hambrienta como si fueran invisibles entre la gente y me he parado con la boca abierta ante los maniquíes más tristes del universo en los escaparates más baratos que lucen lo que sólo pueden comprarse los más pobres. He visto todo esto y mucho más. Pero el ahorita, amigos.... ese ahorita elemental, se me escabulle y cada vez que lo oigo me quedo perplejo preguntándome qué querrá decir quien me lo dice.

13:39
Las mujeres en la Historia de la Filosofía
» ‎ Aprender a Pensar

La Red Española de Filosofía (REF) lanza una campaña durante todo el mes de marzo para difundir la filosofía de pensadoras destacas de la Historia de la Filosofía.

Hannah Arendt

Mujeres que han contribuido de manera destacada a la historia del pensamiento y que, sin embargo, no están presenten en el canon filosófico pese a la influencia y trascendencia que han tenido sus ideas, como por ejemplo, Hannah Arendt.

La REF recomienda en su artículo algunas obras fundamentales y anima a sumarse a su campaña.

Por otro lado, algunas de las filósofas más influyentes de nuestro país recomiendan en este otro artículo a sus pensadoras favoritas, como María Zambrano.

María Zambrano

La nueva Presidenta de la REF, María José Guerra Palmero, nos recuerda: “Nos toca enlazar el pasado con el futuro y éste no es concebible sin la visibilidad y el reconocimiento que debemos a las amantes de la sabiduría, a las filósofas, que ya se vislumbran desde la República platónica dado que el discípulo de Sócrates rompió con la legitimidad del linaje de sangre y apostó por el “aristocratismo” de la inteligencia y del mérito.”

Podemos empezar desde el principio de la Historia de la Filosofía, y para ello recomiendo Historia de las mujeres filósofas de Gilles Menage, un libro que referencia a sesenta y cinco mujeres de la Antigüedad.

La entrada Las mujeres en la Historia de la Filosofía se publicó primero en Aprender a pensar.

11:25
Days without End (#181)
» ‎ telèmac

Els soldats ploraven, però no eren llàgrimes que jo conegués. Altres van llençar els barrets a l'aire, com si fos una celebració boja. Altres es van aguantar el cap com si haguessin sabut de la mort dels seus éssers estimats. No semblava que hi hagués res viu, ni tan sols nosaltres. Estàvem dislocats, no érem allà, ara érem fantasmes.

Aquesta novel·la de 2016, de l'autor irlandès Sebastian Barry, també ha estat una revelació recent. És possiblement una de les millors novel·les que he llegit mai, i tant se val que n'hagi llegit un bon munt a aquestes alçades. Tot i que ha estat unànimement aclamada per la premsa, i amb raó, val a dir que els mecanismes de publicitat de les editorials, que tan omnipresents poden esdevenir quan volen, no li han fet justícia en absolut. Amagar deliberadament el seu argument i la temàtica principal de la contraportada no sembla una estratègia de màrqueting gaire intel·ligent al segle vint-i-u: o bé pressuposa en els potencials lectors tot un bagatge de prejudicis que molt possiblement ja hagi quedat enrere, o bé l'etiqueta "història d'amor homosexual amb rerefons de western" pot evocar connotacions que no tenen res a veure amb el que la novel·la ofereix en realitat. Però és veritat que quan el vaig obrir per llegir-lo per primera vegada no tenia ni idea de què hi trobaria, i que la majoria de publicitat que en vaig llegir esmentava vagament l'ambient històric de la guerra civil americana sense més detall. El relat que Sebastian Barry ens proposa és la història d'amor de dos soldats de l'exèrcit americà, John Cole i Thomas McNulty, a través dels anys. Les seves experiències vitals inclouen la seva participació al genocidi contra els indis i posteriorment en la guerra civil americana, tot i que l'esdeveniment central a les seves vides és l'adopció d'una nena índia, que sense ells saber-ho canviarà els seus destins de formes fortuïtes però totalment decisives. La novel·la és una autèntica revelació no per la història que explica sinó per la seva forma. El que Barry fa a Days without End és recrear una veu històrica silenciada per la ideologia dominant de l'època, i que no pel fet d'haver estat recreada perd en cap moment la seva vivor i el seu realisme. Thomas McNulty és un adolescent irlandès que travessa l'oceà fins als Estats Units en un dels vaixells de la mort, que descobreix que ha de mantenir la seva identitat sexual en secret perquè no encaixa en la societat on viu, però que a la vegada la viu des d'una normalitat completament fluïda, que mai no resulta forçada dins del text. Les decisions dels personatges, les seves motivacions, els seus anhels i passions se'ns presenten amb una solidesa i una lògica que és impossible discutir en el més mínim detall, i d'aquesta forma, Barry ens ofereix una petita gran novel·la americana, un relat sobre la gent que queda aparcada als marges de la història escrita en majúscules, però a la vegada la mouen amb esforços invisibles i silents. A través del seu protagonista Barry desplega una habilitat extraordinària per crear bellesa a través d'una prosa senzilla, sòbria i directa, i un domini del suspens a través del seu argument que et manté en tensió fins a l'última pàgina. El relat ens presenta esdeveniments de cruesa extrema i de violència brutal, però no per això deixa de ser d'una bellesa captivadora, i aquesta contradicció en els termes és part d'aquesta tensió que ens porta a través de la lectura, un pòsit que pots provar de rosegar, si vols, però que al final resulta impossible de digerir.
Sinopsi: A través de les dècades de 1850 i 1860, Thomas McNulty i John Cole creixen com a parella, primer com a transvestits al món de l'espectacle, després a l'exèrcit americà durant les guerres amb els indis i al bàndol del nord durant la guerra civil. En un dels forts on estacionen adopten una nena òrfena, i aquesta decisió els acaba condicionant l'existència de formes completament inesperades al llarg de l'argument. Temps després, quan aconsegueixen establir-se en una granja, els fantasmes del passat acabaran apareixent sempre de les formes més inesperades.
M'agrada: Aquesta novel·la és una autèntica revelació en la seva duresa i la seva bellesa al mateix temps. M'ha agradat com Barry recrea l'ambient de l'època sense sonar en cap moment forçat, com inclou la història dels immigrants irlandesos en la història més gran de la formació dels Estats Units, com retrata la història de les injustícies comeses contra els nadius americans d'una forma clara, sense concessions, completament realista. La forma com construeix l'argument també és un dels punts més forts de la novel·la. Els girs d'argument esdevenen completament inesperats, però a la vegada mantenen una lògica o una inevitabilitat intrínseques que fan de la lectura una experiència totalment colpidora.

11:02
Tercer debat Curs 2017-18: Vivim ara en una època il·lustrada?
» ‎ Comunitat Virtual de Filosofia

Atreveix-te a pensar! Té valor per disposar del teu propi enteniment! Aquest és el lema de la Il·lustració que, segons Kant, suposava que l’ésser humà havia arribat a la majoria d’edat i havia de començar a pensar por sí mateix. … Continua llegint →

9:12
Sin π no soy nada
» ‎ Aprender a Pensar

Por Clara Grima, Presidenta de la Comisión de Divulgación de la RSME.

El futuro se escribe con ‘M’ de matemáticas’. El desarrollo de un país depende, cada vez más, de su desarrollo científico y tecnológico y en ese desarrollo la formación en matemáticas juega, indudablemente, un papel central. Además de ser clave en el crecimiento personal de nuestros estudiantes por su carácter instrumental y las habilidades lógicas y flexibilidad mental que les aporta. Sin embargo, los datos hablan de una tendencia decreciente en las vocaciones científico-tecnológicas y no son pocos los que apuntan a las matemáticas en la lista de factores que contribuyen al alejamiento de los estudiantes de estos perfiles de ciencia y tecnología.

Desde la comisión de divulgación de la RSME entendemos que, cada vez más, se hace necesaria la divulgación de las matemáticas en todos los formatos posibles con el propósito de acercar la belleza y utilidad de las mismas a la sociedad en general, apoyar al profesorado de Primaria y Secundaria en su tarea de enseñar e invitar a los estudiantes a no perderse el delicioso espectáculo de conocer y usar las matemáticas.

Por ello, entre otras acciones divulgativas realizadas a lo largo del año en diferentes medios y canales más o menos habituales, los miembros de la citada comisión nos sentimos especialmente orgullosos del evento que, por primera vez en 2017, se celebró en España el día de π, el 14 de marzo.La respuesta de los centros educativos superó con creces las expectativas y ese día el número π tuvo sus minutos de gloria en casi todos los medios nacionales (prensa, radio y televisión).

La iniciativa, con el lema Sin π no soy nada, fue una idea original de la comisión de divulgación de la Real Sociedad Matemática Española, a la que se sumaron (para su desarrollo) la Consejería de Economía y Conocimiento (CEC) de la Junta de Andalucía, la Fundación Descubre, la Sociedad Andaluza de Educación Matemática Thales (Thales) y la Federación Española de Sociedades de Profesores de Matemáticas (FESPM).

Uno de los grupos de población que más nos preocupa, y que es potencial receptor de las acciones de difusión de las Matemáticas, es el de estudiantes de Primaria, Secundaria y Bachillerato. Entendemos que, como ya se ha dicho, mejorar su formación matemática repercutirá positivamente en el desarrollo posterior de la ciencia y la tecnología de nuestro país y, por lo tanto, en el futuro del mismo. Si bien es cierto que las cinco instituciones mencionadas ya dedican un esfuerzo importante a la organización de eventos destinados a este alumnado, por ejemplo, las Olimpiadas Matemáticas, con ediciones para Secundaria convocada por la Thales y la FESPM y la correspondiente a Bachillerato organizada por la RSME, también lo es que hay un porcentaje, desgraciadamente alto, de niñas y niños y de adolescentes que nunca tendrán ni la actitud ni la aptitud para que este tipo de acciones les sirvan como puente hacia las Matemáticas.

Con esta idea en mente y, aprovechando que desde hace algunos años el 14 de marzo es una fecha cada vez más celebrada en el mundo como el Día Internacional de Pi Day, según la escritura de la fecha en anglosajón (3.14), queríamos organizar un evento alrededor de este maravilloso número irracional destinado a estudiantes de Primaria, Secundaria y Bachillerato, sin necesidad de
que destaquen en Matemáticas.

Este tipo de propuestas de acercamiento a la sociedad en general y al alumnado en particular, que tienen otras aptitudes distintas en relación con las Matemáticas pueden aportar en la mejora de la educación matemática en nuestro país, en la promoción de las vocaciones científicas y en el impulso a la cultura científica en general. Por otra parte, no podemos permitirnos que aún queden tantas personas que no estén disfrutando, como hacemos quienes nos dedicamos a estas tareas, de la belleza del razonamiento matemático. No nos parece justo.

Eso fue en 2017, la buena noticia es que ya se están perfilando los últimos detalles para lanzar el evento correspondiente para marzo de 2018. Este año la fiesta central se celebrará en la Universidad de Salamanca aunque hay previstos eventos alrededor de π en muchos puntos de la geografía española. Y sí, también llevará asociado un concurso de relatos, cómics y vídeos para que nuestros estudiantes combinen su creatividad con la magia de π.

Permanezcan atentos a sus pantallas, a la página y, si son docentes, no duden en invitar a sus estudiantes a esta fiesta tan irracional.

La entrada Sin π no soy nada se publicó primero en Aprender a pensar.
9:10
El juego de Sim
» ‎ Aprender a Pensar

El juego de Sim, perteneciente a la familia de juegos con “lapiz y papel”, es un sencillo juego que encierra una gran riqueza matemática. Fue inventado por el matemático estadounidense, experto en criptografía, Gustavus J. Simmons, mientras trabajaba en su tesis doctoral en teoría de grafos, e inspirado en el estudio matemático de los números de Ramsey. El juego aparece en su artículo On the game of Sim (Journal of Recreational Mathematics, 1969).

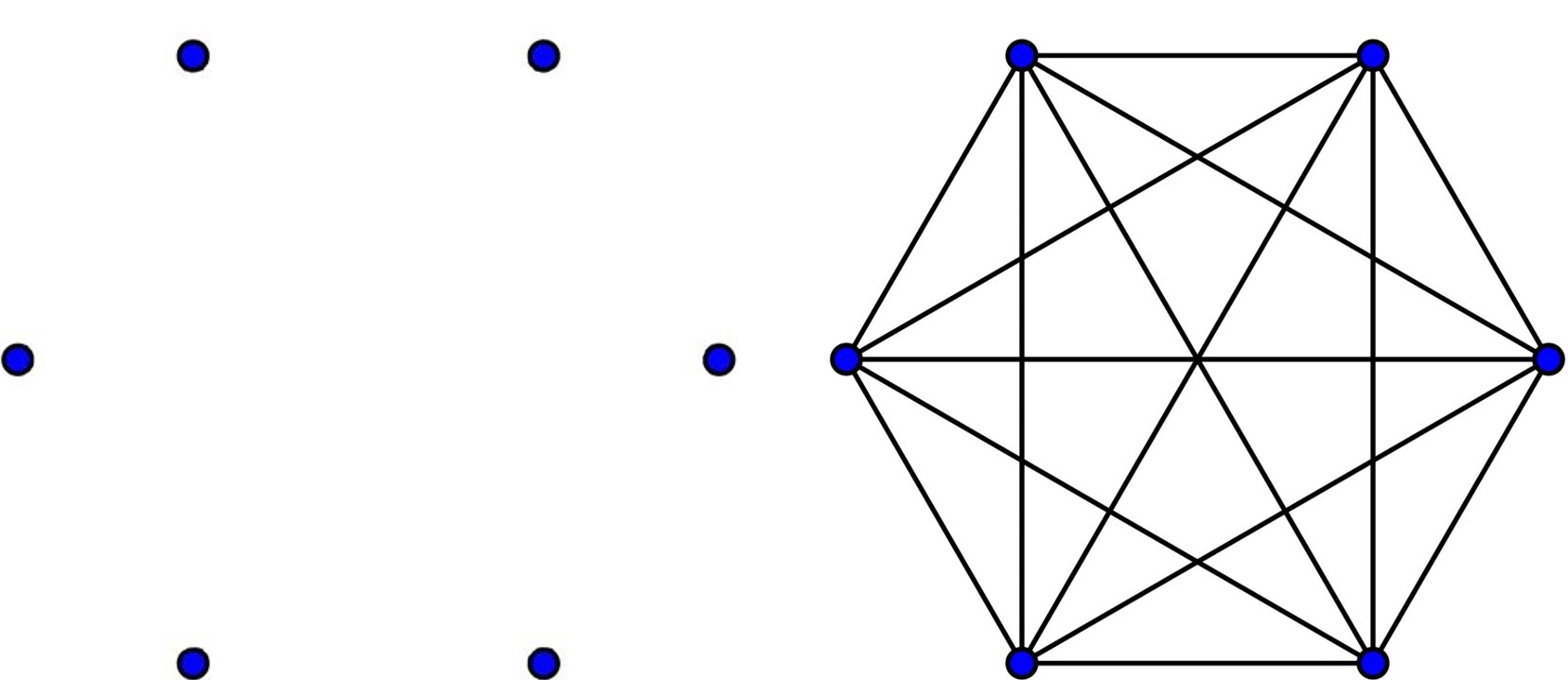
Situación inicial del juego de Sim, con los seis vértices del hexágono, y el grafo completo de seis vértices asociado K6, con los 15 posibles segmentos que unen los 6 puntos dos a dos).

Las reglas del juego son las siguientes. Se consideran los seis puntos que determinan los vértices de un hexágono regular, pintados sobre una hoja de papel. Hay 15 formas distintas de pintar un segmento que una dos vértices de la figura (como se ve en la imagen anterior), que en conjunto forman lo que se llama el grafo completo de seis puntos, K6. El juego de Sim es un juego para dos jugadores, cada uno de los cuales utiliza un lápiz de un color (por ejemplo, azul y rojo) para pintar, por turnos, un segmento que une dos puntos cualesquiera de la figura. Pierde el jugador que primero forme un triángulo monocolor, del color de su lápiz, siendo sus vértices puntos de la figura inicial.

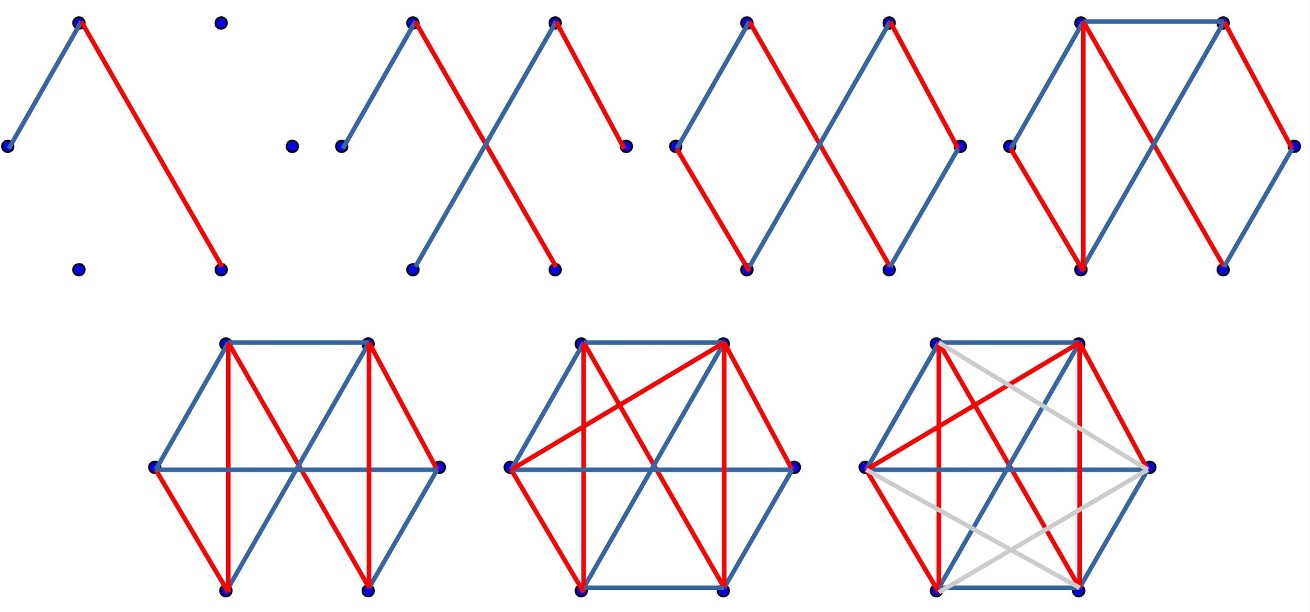
Simulación de una partida en la que el primer jugador pinta con el color azul y el segundo con el rojo. En cada instantánea se observan los dos movimientos de cada turno de ambos jugadores. Pierde el primer jugador, puesto que en el séptimo movimiento, indistintamente del segmento que pinte –en gris en la imagen- formará un triángulo azul con tres vértices del hexágono).

Una característica interesante del juego de Sim es que no puede terminar en tablas, como demostró el propio Simmons en su artículo. La demostración es la siguiente. Consideremos el grafo completo de seis puntos K6 completamente coloreado con los dos colores, es decir, los dos jugadores han continuado pintando segmentos de forma alternada hasta completar el grafo. Tomemos un vértice cualquiera v0. Como hay cinco líneas que pueden unir ese vértice del hexágono con los otros cinco (v1, v2, v3, v4, v5 en la siguiente imagen), como solamente disponemos de dos colores para pintar, al menos tres de ellas son del mismo color, por ejemplo, azul.

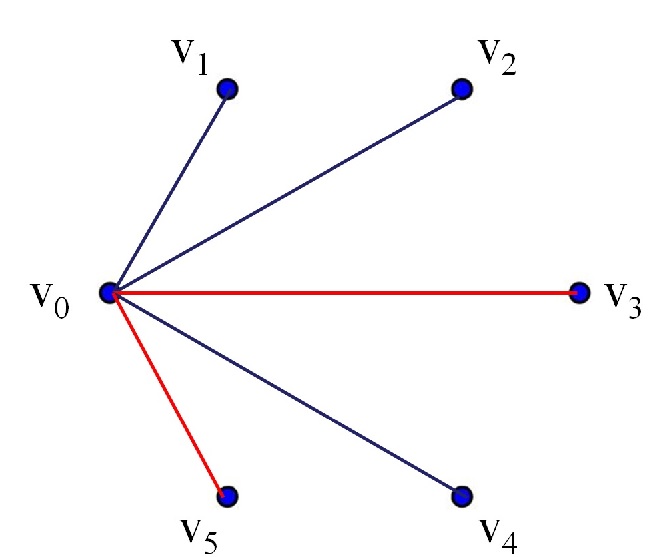
Si alguno de los tres segmentos que unen los vértices finales de esos tres segmentos azules, fuese también azul, entonces formaría un triángulo azul con los correspondientes segmentos azules que empiezan en el vértice v0. Pero si, por el contrario, ninguno de esos tres segmentos es azul, entonces los tres son rojos y forman un triángulo rojo. Por lo tanto, siempre existe un triángulo monocolor, ya sea azul o rojo. Lo cual completa la demostración.
Como consecuencia del anterior razonamiento, no existe la posibilidad de empate en el juego del Sim y alguno de los dos jugadores ganará. Sin embargo, el problema de quien de los dos jugadores tiene una estrategia ganadora y cuál es esta, es bastante complejo. De hecho, Simmons no lo incluía en su artículo, y solo después de un exhaustivo análisis con ordenadores descubrió que es el segundo jugador quien tiene una estrategia ganadora, aun así, esta no es fácil de llevar a la práctica, como ocurre con otras estrategias ganadoras que han ido descubriendo los matemáticos.
La idea que subyace al juego del Sim se enmarca dentro de la Teoría de Ramsey, esa teoría matemática del campo de la combinatoria que viene a decirnos que el desorden completo es imposible, y más concretamente está relacionada con los números de Ramsey.

La entrada El juego de Sim se publicó primero en Aprender a pensar.
9:00
El problema de resolver problemas
» ‎ Aprender a Pensar
Por Javier Bernabeu, editor del Equipo de Matemáticas de SM.
¿Es lo mismo razonar que resolver problemas? Datos – Operación – Solución
Datos, operación y solución son esas tres columnas que habitualmente pedimos a los niños que escriban antes de comenzar a resolver cualquier problema de matemáticas. Es frecuente también que les pidamos que copien el enunciado (no sin pocas quejas por su parte). Pero ¿es verdaderamente importante ser fiel a esta estructura?

1. ¿Qué se supone que pretendemos con esto?
Se supone que con esto los profesores pretendemos que presten atención a los datos, que seleccionen la información necesaria, que descarten lo que no es relevante. Seguidamente, con esta información que han extraído en forma de datos, se supone que los niños tomarán decisiones que les permitan elegir la operación adecuada (en caso de que sean problemas con operaciones) para, finalmente, escribir de forma argumentada la solución del problema en cuestión.

2. ¿Qué pasa en realidad?
Pero la realidad es bien distinta. Lo que ocurre frecuentemente es que los niños dedican más tiempo a ese formalismo de rellenar cosas en las columnas datos-operación-solución que a lo verdaderamente importante, que es el proceso de razonamiento. Acaban copiando casi de manera literal lo que pone en el enunciado en la columna de datos para, seguidamente, tratar de descifrar esa columna de datos. En muchos casos ocurre algo así:

Si queremos dedicar tiempo a hacer a los alumnos conscientes de los datos del problema quizá, en vez de hacerles copiar algo que ya tienen unos centímetros más arriba, deberíamos decirles: “¿Esto de qué va?¿Qué cuenta esta historia?”. Y no:”¿Esto cómo se resuelve?”.

Demasiado esfuerzo han hecho ya copiando un larguísimo enunciado que alguien se ocupó previamente de copiar en un libro. Demasiado esfuerzo invertido en no olvidar saltarse los 6 cuadraditos desde arriba. Demasiado esfuerzo dedicado a recordar que entre línea y línea van dos líneas de cuadraditos. Demasiado esfuerzo realizado para recordar que hay que respetar los márgenes.

No seré yo quien diga que los cuadernos no deben estar limpios y ordenados, pero lo cierto es que, en muchas ocasiones, copiar un enunciado tiene el propósito de facilitar al niño la comprensión del mismo, cuando la realidad es que ha prestado tanta atención a factores estéticos que la comprensión pasa a un segundo o tercer plano.

3. ¿Qué debería pasar?
Si dedicamos un momento a responder ¿esto de qué va?, luego podríamos decirle: “¿Eres capaz de dibujar la historia? ¿Eres capaz de representar pictóricamente esta historia?”. Si hemos dedicado mucho tiempo a hablar sobre de qué va, es fácil pintar de modo esquemático qué cuenta la historia. Y suele ocurrir… ¡algo mágico!

El modo en que indican de qué va lleva implícito la recogida de datos y, en muchos casos, la manera de resolver el problema. Solo nos quedará escribirlo de forma matemática. Algo así es lo que pasa si dibujan de qué va el problema:

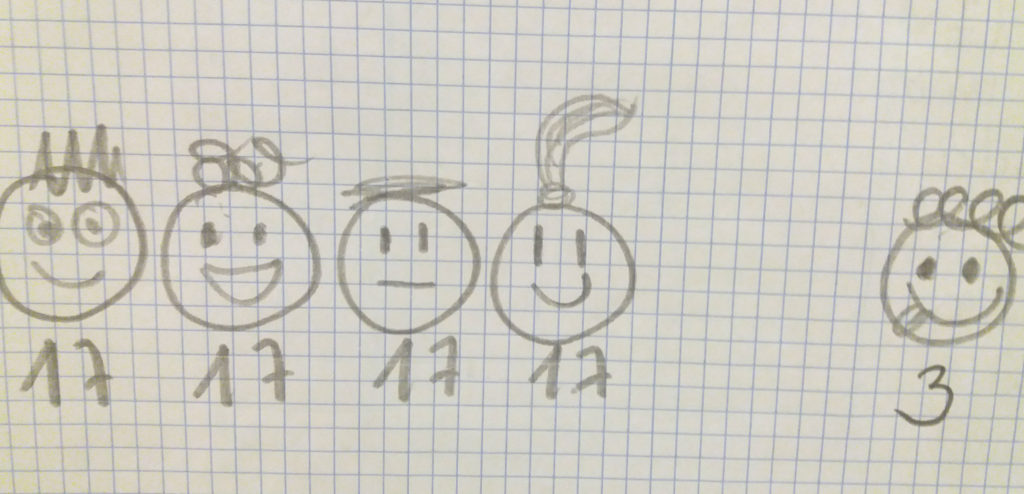
Después del dibujo anterior, el alumno (de 3.ºEP) verbalizó: “4 veces 17 más 3”, y escribió: “4 x 17 + 3”. El alumno no había aprendido aún la jerarquía de las operaciones, pero lo resolvió sin dificultad, ya que el proceso razonado le llevó por un camino correcto.

Horror: confundimos comprensión lectora con razonamiento
Un niño de tres años es capaz de razonar, es capaz de resolver situaciones de esas que se llaman “problemas”, sin embargo, no sabe leer. Entonces, ¿el niño que no tiene suficiente madurez lectora está condenado a no enfrentarse a resolución de problemas?

¡Qué típico es decir que “el niño no entiende un problema hasta que se lo lee el adulto”! Pero si lo resuelve directamente él solo, está claro que ese niño no tiene un problema de razonamiento; lo que tiene es un problema de madurez lectora. Sin embargo, el pobre, tiene que ver cómo en ese ítem del boletín de notas pone “insuficiente”.

¿Es justo que un niño que resuelve bien los problemas si tú se los lees “suspenda” un ítem llamado habitualmente en los boletines “razonamiento matemático”? Si lo que se mide y evalúa es el razonamiento y él razona bien, ¿por qué suspende?

Los problemas deberían ser suyos
Los libros de matemáticas están llenos de problemas que siempre tratan de repartir bolas o caramelos, comprar lápices, calcular descuentos o llenar tazas. Estos problemas reflejan la mentalidad del adulto que pretende adaptarse al interés de los niños o bien hacerles compartir el suyo propio.

En realidad, no están para nada próximos a la realidad del niño. Un problema no es cercano porque trate de pokemon o de cromos o de parques con columpios o del juguete de moda. Para ser cercano a la realidad, un problema debería referirse a su realidad, la realidad de sus cabecitas. Debería ser suyo, inventado por él.

– “¡Pero es que no tienen ningún sentido! ¡Es qué se inventan cada chapuza!”, comentarían algunos.

Problema de Clara (6 años)

Me han regalado por mi cumpleaños dos regalos. El primero costaba 12 euros y tenía dentro un cuento de Caperucita. El segundo costaba 7 euros y dentro había una caja de acuarelas, pero la pastilla de color verde estaba rota. ¿Cuánto costaron mis regalos?

¡Resulta que para Clara es importante contarnos que la pastilla verde estaba rota! ¿Cómo no ponerlo en el enunciado? Otra cosa es que ese sea uno de esos datos innecesarios para la resolución, aunque no por ello deja de ser importante para Clara.

Clara, al inventarse el problema, asume que, no todo lo que se cuenta en él es necesario para responder a la pregunta que se ha inventado, por lo que ella sola descubre que, en función de la pregunta, puede que haya datos no necesarios.

¿Si no todos aprendemos igual, debemos resolver problemas todos igual?

De un depósito lleno de agua se saca la tercera parte del contenido. Después, la mitad del resto y aún quedan 1200 litros de agua dentro, ¿qué capacidad tiene el depósito?
- Si obligásemos a todos los alumnos a ir por la vía datos-operación- solución para resolverlo, el problema tendría cierta complejidad.
- Pero probad a resolverlo numéricamente, sin apoyo gráfico. ¿Resulta complicado?
- Probad ahora a resolverlo dibujando. Quedaría algo así:
Pues imaginad si, en lugar de pintarlo, establecemos el folio como depósito, cortamos la tercera parte y la mitad de lo que queda. Nos acabamos quedando en la mano con un trozo de papel llamado “1200 litros”. ¿Cuál es la capacidad del depósito?

¿Ese niño que no ha puesto datos-operación- solución, pero que acaba con un papel llamado “1200 litros” en la mano, razona?

Como siempre, luego ha de llegar el momento en que traduzcamos a idioma matemático lo que ha pensado con ayuda de sus manos, pero es clave que la estructura datos-operación- solución no sea más importante que el propio razonamiento.

Y a la hora de elegir los problemas, si es que son elegidos por nosotros, no olvidemos que:

Un problema lo es si realmente si constituye un problema para la mente.

La entrada El problema de resolver problemas se publicó primero en Aprender a pensar.

7:15
La crítica sentimental.
» ‎ La pitxa un lio

De todo lo anterior se infiere que no hay justificación para renunciar a la comprensión de nuestras emociones; y que, como en el caso de las opiniones, tampoco hay por qué no exigir las razones de ellas, sobre todo teniendo en cuenta su gran poder motivador al ser fuerzas impulsoras de acciones que pueden tener importantes consecuencias no únicamente para los que las sienten. Téngase en consideración que los sentimientos y los sistemas de creencias se hallan intrínsecamente vinculados por un bucle psíquico de retroalimentación; que la situación real que puede suscitar un determinado afecto se puede ver impregnada ella misma de emotividad desde las creencias en las que el sujeto está. En el sentimiento, como en la opinión puede anidar el error. El fenómeno psíquico de la disonancia cognitiva, señalado por primera vez en 1957 por Leon Festinger, conlleva el reconocimiento de la fuerza del susodicho bucle, así como la existencia del componente afectivo de las actitudes, que tienen su sustento en un sistema de creencias. Uno puede tomar conciencia de que se equivoca sintiendo lo que siente; experiencia clave para una plena vivencia de la propia libertad.
No hieras mis sentimientos puede equivaler a no te metas con mis creencias. Entonces proteger institucionalmente determinados sentimientos no es sino proteger determinadas creencias. Cuando se condena –pudiendo llegar incluso a la sentencia judicial– a alguien por expresiones más o menos artísticas y/o humorísticas respecto de símbolos religiosos (desde las caricaturas de Charlie Hebdo, pasando por el montaje fotográfico del joven de Jaén hasta las vírgenes de una drag queen carnavalesca) por considerar que se hiere determinados sentimientos se incurre en discriminación hacia otros; por ejemplo, los de miles de ciudadanos a los que la administración niega permisos y colaboración para hallar los restos de sus familiares asesinados a causa de la brutal y sistemática represión franquista. Diríase, entonces que, de modo escasamente razonable, se institucionaliza una categoría de sentimientos que es lícito herir, mientras que otros no. Los primeros serían parte de lo sagrado. Lo sagrado se delimita mediante las creencias perlocutivas, es decir, aquellas cuyos efectos sobre la realidad provienen del simple hecho de ser proclamadas o negadas (algo es pecado cuando la instancia competente afirma que lo es: integrismo perlocutivo); su territorio se reconoce porque en él está proscrito hacer chistes, pues lo sacro –que no se reduce a lo religioso– es intocable, no se deja sobar por el examen crítico. ¿Y acaso no es el humor uno de los modos de expresión de la inteligencia emocional a cuyo través puede la razón conmover y tornar pensables los afectos?
Terreno, en fin, ricamente abonado para el fanatismo es lo sagrado. Sentimiento que emponzoña el alma y enturbia el juicio de realidad, único cauce a nuestra disposición a través del cual podemos tomar decisiones sensatas. Por nuestros afectos podemos ser manipulados sin ser conscientes de ello. Se precisa de la crítica de los sentimientos –aunque en ocasiones conlleve herirlos sin remedio– si se desea salvaguardar la propia libertad, que exige el conocimiento de los hilos internos que accionan los resortes de nuestro espíritu.
José María Agüera Lorente, No hieras mis sentimientos (¡son criticables los afectos!), Filosofía en la red 11/03/2018 [www.filosofiaenlared.com]
7:07
Són els sentiments respectables?
» ‎ La pitxa un lio

Hoy sabemos que la idea del individuo como sujeto racional es eso, una idea; con algo de mito en tanto en cuanto hay quien todavía es presa de lo que Edgar Morin llamaba «la autoidolatría del hombre que se admira en la ramplona imagen de su propia racionalidad». En este sentido el error de Descartes, que es el tema recurrente del libro del neurocientífico Antonio Damasio titulado precisamente El error de Descartes, consiste no sólo en la apuesta por el dualismo psicofísico sino también en el encumbramiento de una racionalidad pura e idealizada al margen de toda afectividad. La prueba –para mí definitiva– de lo errado de esa concepción nos llega del mundo de la economía, en el que, si se quiere ser congruente con los hechos, se ha de aceptar sin más remedio que el sujeto racional no es más que un modelo ideal que puede ser útil como recurso hipotético según parece demostrar la reciente crisis financiera global.

Hay que contar con los sentimientos, ciertamente. El ya fallecido psiquiatra Carlos Castilla del Pino en su Teoría de los sentimientos establecía que «los sentimientos son algo de lo que se vale el sujeto, merced a lo cual apetece de los objetos (y de sí mismo), se interesa por ellos (para hacerlos suyos o alejarlos de sí) y, en consecuencia, se hace en el mundo, en la realidad psicosocial». Seguramente por eso, o más bien por cierta impronta humeana, definía Bertrand Russell la vida buena como «la inspirada por el amor y la guiada por el conocimiento» (léase su ensayo al respecto en su libro Por qué no soy cristiano). Dice el filósofo, en congruencia con la tesis del psiquiatra, que el amor es más importante que el conocimiento, ya que otorga el impulso que se requiere para desear conocer. La misma filosofía en su propia plasmación nominal contiene el reconocimiento de lo dicho, pues es amor o deseo de saber lo que hace de ella algo vivo.

Una vida puramente racional sería tan sosa. La salsa de la vida son los sentimientos, porque un sujeto sin sentimientos sería un sujeto sin conflicto, es decir, un ser apático, que no estaría activamente en la realidad, ya que nuestra relación con ella es esencialmente conflictiva a lomos de un pertinaz deseo, unas veces de apropiación de esa realidad, otras de rechazo; todo lo cual lleva al individuo a modificarla en ocasiones y hasta a destruirla. «Por eso –concluye Castilla del Pino–, al ser el sujeto una "máquina" de desear objetos, su relación con la realidad es necesariamente conflictiva: quiere lo que no tiene; y si lo tiene, teme perderlo. Además de verse obligado a contar con lo que no desea tener».

Eso incluye a los demás, porque la realidad incluye a los demás. Y los demás pueden no sentir lo que nosotros hacia determinados objetos como la patria o nuestra fe religiosa o el equipo de nuestros amores. A este respecto parece ser que existe un derecho a que a uno no le hieran sus sentimientos, como hay desde hace tiempo ese absurdo lema según el cual todas las opiniones son respetables. Cada cual tiene derecho a pensar lo que quiera, y se le tiene que respetar; congruentemente, cada cual tiene derecho a sus sentimientos, y que se respeten, lo que suele incluir para muchos que no se hieran. Esto último muy coherente a mi parecer con la idiosincrasia propia de la democracia romántica. En verdad, si hay una necesidad de que se respeten las opiniones de todo el mundo es porque argumentar razonablemente en contra de ellas se tiene ya por equivalente a herir los sentimientos de quien las sostiene. Ahora bien, ¿son todos los sentimientos respetables? ¿Deben y pueden los sentimientos de cada cual quedar al margen de toda crítica? ¿Hay acaso sentimientos de algunos que, por su estatus especial, deben quedar a salvo de cualquier expresión que pueda herirlos?

José María Agüera, No hieras mis sentimientos (¿son criticables los afectos?), Filosofía en la red 11/03/2018

[www.filosofiaenlared.com]
6:58
Els problemes de la filosofia actual.
» ‎ La pitxa un lio

La filosofía debe, si no quiere verse cada vez más arrinconada en una autocontemplación narcisista, retomar como tarea fundamental la reflexión sobre los problemas que inquietan a los seres humanos en el momento presente, como supo hacer en otros momentos en que gozó de mayor consideración. En realidad, puede decirse sin exageración que los problemas principales que tiene la filosofía ante sí al día de hoy son probablemente los más graves y más difíciles de todos aquellos a los que ha tenido que enfrentarse a lo largo de su historia. A título de ejemplo, he aquí algunos de los que creo de más interés:(1) ¿Qué consecuencia ha tenido sobre nuestro planeta el desarrollo tecnocientífico e industrial, y qué alternativas hay a lo que estamos haciendo con él? ¿Hay posibilidad de mantener una actitud nueva ante la tecnología? ¿Qué relación queremos mantener con los demás animales y con la naturaleza en general? ¿Qué responsabilidades tenemos con las generaciones futuras?(2) ¿Qué cambios han de producirse en la comprensión de nuestra propia especie ahora que empieza a vislumbrarse su posible su transformación biotecnológica? ¿Querríamos ser sobrehumanos o posthumanos a través de la genética? ¿Querríamos ser inmortales si estuviera a nuestro alcance esa posibilidad?(3) ¿Cómo va afectar todo esto a nuestros modos de ordenación política y social y qué podemos hacer para que el resultado sea más justo y proporcione mayor libertad e igualdad? ¿Cómo vamos a hacer que los beneficios del progreso científico y técnico estén orientados realmente al bienestar de todos los seres humanos, empezando por los más desfavorecidos?Antonio Diéguez, El valor de la filosofía, Centro de Estudios Filosóficos, Políticos y Sociales Vicente Lombardo Toledano marzo 2015 [www.centrolombardo.edu.mx]
6:55
Stephen Hawking i el futur de la filosofia.
» ‎ La pitxa un lio

Stephen Hawking se desmiente casi inmediatamente a sí mismo, cuando en las mismas entrevistas en que dice que la filosofía ha muerto (inicialmente lo sostuvo en su libro El gran diseño), añade que debemos manipular nuestros genes para convertirnos en seres superinteligentes capaces de competir con las máquinas superinteligentes que crearemos dentro de poco. ¿No hay ninguna cuestión filosófica relevante detrás de esta pretensión? ¿No hay presupuestos discutibles desde la epistemología, la ética, la antropología filosófica, la filosofía de la mente…? No parece que haga falta esforzarse mucho para reconocer varios.Pero dicho esto, hay que añadir a continuación que la filosofía no tiene garantizado un futuro. De hecho, presenta síntomas claros de decaimiento –que son en buena parte causantes de su deteriorada imagen– de los que cabe responsabilizar a los propios filósofos. A lo largo del siglo XX, uno de los siglos más convulsos de la historia, la filosofía (con algunas excepciones notables) pensó que podía desentenderse de los problemas que verdaderamente aquejaban a la humanidad. Pensó que le estaban reservadas tareas más elevadas, más nucleares, menos periféricas. Se replegó entonces en disquisiciones escolásticas sobre la conciencia pura, el lenguaje ideal, el modo en que hablamos de ciertas cosas, la interpretación infinita de significados textuales, el final de la filosofía, la muerte del sujeto, la construcción social de la realidad. Se obsesionó con el rigor puramente formal y con la elaboración de una jerga aparentemente rompedora, pero incomprensible. Se hizo académica, en el peor sentido de la palabra, y dejó las cuestiones importantes en manos de opinadores diversos y de “think tanks” a sueldo. Con todo ello, ha dejado tras de sí un largo reguero de ideas vacías, como las ha llamado Peter Unger, que solo han interesado a los ingresados en cada una de sus especializadas escuelas. No es extraño, pues, que ante la constatación de este estado, se hayan multiplicado las voces de los que certifican que la filosofía ha muerto, justo en la época en que más se escribe y se publica sobre filosofía.La filosofía –es verdad–, a diferencia de las ciencias, no hace descubrimientos; excepto uno solo, y cuando es buena: nos pone al descubierto lo que los seres humanos hemos sido y lo que hemos querido ser. Nos señala cuáles han sido nuestras aspiraciones y nuestros miedos, nuestros deseos y nuestros deberes, nuestros límites y nuestra desmesura. Eso es básicamente lo que cualquier estudiante de filosofía aprende a valorar a través de numerosas lecturas en los años de su formación. Pero aprende también algo aún más valioso que difícilmente aprenderá en otros lugares, ya sean académicos o no, a saber: que si bien a lo largo de la existencia uno puede ponerse, si quiere, en las manos de muchos guías morales o intelectuales, sólo el uso autónomo de la razón, como nos enseñó Kant, hace a un ser humano alguien auténticamente libre. Por eso, el estudiante de filosofía, al cabo de un tiempo, no podrá ya enfrentarse a ningún asunto importante en su vida sin considerarlo al modo filosófico, es decir, sin preguntarse qué le dice al respecto su razón. Esto le traerá ventajas en algunas situaciones, porque no son muchos los que se atreven a salir de la opinión común, de lo que se supone que debe pensarse sobre ese asunto. Y podrá así aportar un punto de vista diferente. Pero le acarreará también desventajas. Sobre todo en aquellos momentos en los que el sentido de lo práctico, de lo conveniente, ha de ser pospuesto. Y es que, paradójicamente, el lado no teórico, sino práctico, de la filosofía –el que ha tenido siempre como fin último el logro de una vida digna de ser vivida–, ha aconsejado repetidas veces al practicante de la filosofía ser poco práctico. Todo el que se dedica profesionalmente a la filosofía ha de preguntarse alguna vez si merece la pena seguir este consejo.Antonio Diéguez, El valor de la filosofía, Centro de Estudios Filosóficos, Políticos y Sociales. Vicente Lombargo Toledano marzo 2015
[www.centrolombardo.edu.mx]

← marzo 13 (6 temas) marzo 15 (5 temas) →

BLOCS DE FILOSOFIA » marzo 14, 2018

Canales

(11 sin leer)