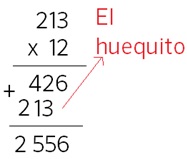
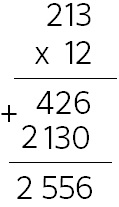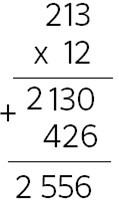14:02
»
Educación y filosofía
14:02
»
Educación y filosofía
Normal 0 21 false false false ES X-NONE X-NONE /* Style Definitions */ table.MsoNormalTable {mso-style-name:"Tabla normal"; mso-tstyle-rowband-size:0; mso-tstyle-colband-size:0; mso-style-noshow:yes; mso-style-priority:99; mso-style-parent:""; mso-padding-alt:0cm 5.4pt 0cm 5.4pt; mso-para-margin-top:0cm; mso-para-margin-right:0cm; mso-para-margin-bottom:10.0pt; mso-para-margin-left:0cm; line-height:115%; mso-pagination:widow-orphan; font-size:11.0pt; font-family:"Calibri","sans-serif"; mso-ascii-font-family:Calibri; mso-ascii-theme-font:minor-latin; mso-hansi-font-family:Calibri; mso-hansi-theme-font:minor-latin; mso-fareast-language:EN-US;}
Walter Benjamin, escritor revolucionario. Lectura de Susan Buck-Morss.
Marcos Santos Gómez
Seguimos tratando de comprender en qué consisten exactamente una filosofía y una pedagogía revolucionarias. Para ello nos centramos ahora en el a menudo críptico y difícil pensamiento de Walter Benjamin, tal como lo fue desarrollando en sus obras postreras, con especial atención al voluminoso y desconcertante Libro de los Pasajes. Como es sabido este consta fundamentalmente, en un setenta u ochenta por cierto, de citas extraídas de las más variopintas fuentes de mediados del siglo XIX, cuando el esplendor del mundo burgués y su cultura en el París que abrió sus “pasajes” era aún incipiente en algunos de sus desarrollos culturales, aunque era ya dueño definitivo de la civilización. Es decir, Benjamin se fijó en un momento concreto de la historia de París que expresaba el ascendente predominio de una cultura y civilización burguesas, que daba las pistas de lo ya que estaba instalado en la sociedad o todavía en parte quedaba por venir. Podemos entender que el final de todo aquello sería el tiempo quietoque vivimos, en el que ya no avanza la historia, salvo la tecnología que crea en su avance la ilusión de movimiento, de cambio de aquello que en realidad permanece siempre igual. La crítica histórica de Benjamin compondría una de las variantes de la denuncia de un horror tecnológico que distintas perspectivas filosóficas del siglo XX han emprendido, el terror de una idea de progreso que parece cubrir con oropeles el espanto que sucede a su paso. Se trata del tiempo muerto, como es evidente, de la actual sociedad de consumo, en el que todo cambia para permanecer igual.
Pero vayamos por partes, procurando un imposible afán de sistematizar lo que Benjamin entendió que solo puede decirse fragmentariamente.
En París se dieron a lo largo del siglo XIX varias revoluciones importantes (1830, 1848 y 1871) y era el prototipo de la ciudad y la cultura burguesas. Ese momento, hacia mediados de siglo, anterior a la Comuna de 1871 y correspondiendo con el Segundo Imperio de Napoleón III y las reformas urbanas de Haussman, inventó lo que hoy sería para nosotros los centros comerciales o los parques temáticos. Entonces, como hoy la idea del centro comercial, el invento (nacido realmente en la década de los años 20 del siglo XIX aunque su esplendor llegaría, como hemos dicho, hacia la mitad del siglo) consistió en la construcción de espacios urbanos que proporcionaban una suerte de sedación narcotizante mediante la sobreestimulación de los sentidos, en los que se vendía de todo masivamente. Con la saturación sensorial procedente del mundo de las mercancías, lo estético conducía a lo anestésico, en palabras de Buck-Mors, lo que dicho de otro modo encarna una paradoja curiosa: la misma estructura social que impedía la satisfacción de una vida lograda, es decir, la que despojaba y despoja a los hombres de la oportunidad de realizarse, administraba, como si fuera una droga, más de sí misma, apoyándose en los sentidos pero para crear una irrealidad con visos de doble realidad. Es decir, los sentidos, instrumento de la captación sensible del mundo y base, por tanto, del realismo, eran la vía de entrada de un descomunal espejismo que acompañaría a nuestra percepción del mundo hasta los días actuales. Paradójicamente, un mundo añadido, sombra y reflejo del mundo real, asumiría mayor consistencia ontológica para los hombres. Un ficticio mundo de placer que como una ensoñación constituiría las veces del mundo por el que las personas ayer y hoy paseamos. Un mundo doble cuya verdad se basa en el engañoso placer capaz de proporcionar y en la construcción a partir de esta seductora y apetecible red de estímulos de una ingente y colectiva falsa conciencia. Falsa conciencia porque torna real lo que es de origen irreal, es decir, la sombra o el espejismo por el modelo, y porque produce también la ilusión de realización mediante aquello que, justamente, nos priva de una realización auténtica.
Los pasajes parisinos, de los que hoy no queda ni rastro (aunque recuerdo haber visitado algunas galerías de ese tipo en la ciudad de Milán, como lugar comercial y turístico), eran calles en las que lo privado se hacía público, pues ellas mismas eran calles de libre circulación peatonal (no entraban los carruajes) a las que se había cubierto con cristaleras y soportes de hierro proporcionando una sensación de interior e intimidad. En ellas paseaban tanto burgueses como vagabundos, prostitutas y maleantes, en un ritual voyeur de contemplación de cuantos objetos se exponían en tiendecitas, superpuestos, ajenos ya prácticamente a toda función que no fuera su estatuto decorativo, su existencia destinada a ser mirados e imaginados adornando el propio hogar. Allí el tiempo quedaba en suspenso, como reflejó la moda de sacar a pasear grandes tortugas (lo que en el centro de las ciudades actuales tomadas por la prisa y los automóviles, sería imposible). Eran estas galerías callejeras además una suerte de personificación de cómo lo estructural, lo público, lo que se da en las relaciones entre los seres humanos, se introducía en un mundo privado de sensaciones amenas y se transmutaba en ello. La estructura se internalizaba y subjetivaba.
Benjamin se fija especialmente en las personas que llama flaneurs, que eran quienes, como los mendigos o vagabundos, pasaban allí sus días intentando trapichear o simplemente caminando sin rumbo, sin tiempo, en una rutina de contemplación puramente ociosa. De algún modo Benjamin pensaba que allí el mundo capitalista se contemplaba a sí mismo, en el apogeo de la ensoñación que le es propia, pero al mismo tiempo las mercancías, captando la atención como fetiches, idealizadas, erotizadas (se daba una intensificación de las sensaciones, una saturación de los sentidos, como por ejemplo las impresionantes perfumerías allí presentes, los buenos restaurantes que ya estaban de moda, la ingente oferta de placeres sexuales que vendían los numerosos prostíbulos o las eternas ristras de telas y sedas de infinidad de texturas que podían tocarse infinitamente), más allá del mero valor de uso y adquiriendo por tanto nuevos precios basados en el puro valor de cambio, sugerían, en lecturas a menudo inconscientes, el carácter de ensoñación de todo aquello.
Quizás uno era atrapado en aquel juego, pero al mismo tiempo se ofrecía la posibilidad en ciertas circunstancias de vivirlo conscientemente. Uno podía darse cuenta de que lo expuesto tenía una utilidad de la cual se había despojado. Y quienes antes percibían esto, el dinamismo del llamado por Marx “fetichismo de la mercancía” por el que las mercancías nublan y ocultan con su glamour lo que verdaderamente hay tras ellas, es decir, el mundo del trabajo y la producción o incluso su simple utilidad directa, eran los vagos, los ociosos, los vagabundos, los pobres, las “busconas”, que desde su desafiante ocio vital, fuera del horrible mundo de la esclavitud laboral y por tanto como seres marginalmente críticos, percibían mejor el carácter de fantasmagoría de todo aquello. Ellos flotaban, literalmente, en el sueño colectivo, como sonámbulos. Seres que no querían ni podían comprar, fuera de los circuitos de la economía, que, contra la idea de Marx respecto al lumpen (proletarios fuera de la cadena laboral, como excrecencias o sobrantes sociales sin función ni visión ninguna que, según Marx, no podían encabezar ninguna transformación revolucionaria), para Benjamin eran la clave, justamente por su libertad en relación al mundo del trabajo.
Quizás Benjamin mantuvo esa especie de simpatía por los más excluidos entre los excluidos, por los seres totalmente marginales y los desechos sociales que ni siquiera se integraban como eslabones de la cadena de la producción capitalista. Irónicamente, me atrevería a decir que su estatuto era, y es acaso hoy, el de una aristocracia invertida, ociosa y con la posibilidad de desarrollar valores y perspectivas que quienes vivimos dentro del sistema, no tenemos. Saben del horror, lo padecen cruelmente y son por él desfigurados, por supuesto, pero pueden mirarlo desde fuera, cosa que la mayoría no podemos hacer, aunque de una manera intuitiva, como si presintieran la trampa. Acaso un raro y odioso privilegio, encarnado en la más pura y rabiosa negatividad del punky actual. En este mundo al revés, como señala la verdad bíblica y cristiana, los últimos son los primeros. Y la conciencia, en su trabajosa constitución, emerge incipiente y dudosa antes en ellos que en nosotros, por eso mismo, por ser quienes están fuera de la oleada consumista que nos mantiene atrapados material e ideológicamente al resto.
Como por arte de magia aparecía en las mercancías expuestas de los pasajes un valor simbólico, ideal, que no era el que correspondía a su uso. Es decir, en aquellos pasajes el burgués y el obrero entraban, literalmente, en una misma ensoñación que constituía el sumun de la cultura capitalista-burguesa. Recordemos que los sueños tienen para Benjamin una doble característica, de expresión de deseos frustrados o de sufrimiento y pesadilla por el malestar sufrido en el mundo capitalista. La primera y más obvia es aquella expresada por gran parte de la literatura burguesa a partir del Renacimiento, desde las utopías como género literario, por la que el mundo tendría un carácter sublime, pero ficticio, en el que lo más real sería lo que habita entre las ideas, en el mullido confort de la cultura, que va superponiéndose a las relaciones reales, materiales, entre los hombres. Hay una especie de segundo mundo superpuesto, edulcorado, en el que se viven sueños que el mundo burgués no puede lograr. Es decir, lo propio de la burguesía es soñar aquello que sabe, inconscientemente, que no puede ser invocado en la realidad y que por tanto jamás va a obtener. Quizás algo semejante a lo que veíamos en entradas anteriores que García Rúa achacaba a la literatura utópica del Renacimiento, es decir, el constituir una fábrica de sueños (curiosamente así se ha llamado algunas décadas más tarde al cine) que no afectan al mundo real, porque se parte de un hondo desdoblamiento fundamental entre los hechos y la historia, por un lado, y los ideales y los sueños. Algo así como el monstruo de unos ideales, que por cierto yo tanto he elogiado como horizontes para la educación, pero unos ideales que no tocan en este caso, ni afectan, a la realidad, porque no están conectados con lo que en ella puede hacerla cambiar. Estos planos ideales no incluyen lo que básicamente produce la necesidad de trazar dichos sueños e ideales, es decir, su causa, su origen social y estructural. Les falta su materia y se han estrechado a un nivel formal.
Así el misticismo y la presencia de una cultura vaporosa, sin pies en la realidad pero gratificante, donde el burgués y el obrero pueden consolarse de su miseria “juntos”, impregna nuestro mundo. Algo que, miedo nos da, parece también representar a la escuela y al mismísimo ideal de la escolarización. Una suerte de amalgama social que es homogeneizada desde un loable afán de justicia y libertad, pero que, como señalan los estudios de Bourdieu, no afecta en absoluto a la realidad dividida que existe fuera de sus muros, con sus juegos de intereses. Aun más, supone una ilusión que refuerza el carácter escindido de la sociedad humana, que incluso lo fabrica cubriéndolo con un neutro velo de equidad y justicia social.
Según la teoría del fetichismo de la mercancía que explicara Marx, vivimos en ese sueño por el que las cosas valen a partir de fenómenos sociales de explotación o especulación que escapan a su valor real, a lo que él llamó, en El capital por ejemplo, “valor de uso”. Contra lo que también hoy se nos hace creer, que las mercancías valen realmente el precio estipulado, basado, supuestamente en su utilidad y el trabajo empleado en hacerlas, su mera presencia y su precio ostentan sin embargo la condición de fantasmagoría, es decir, se basan en una mistificación por el que la mercancía se tiñe de simbolismo, erotismo y virtudes que son las que de verdad están detrás del atractivo que ejercen para nosotros. Nos atraen sin saber siquiera qué nos traemos entre manos, como ocurre con los narcóticos o el opio. Repito, apelo a la fascinación universal por los grandes y suntuosos centros comerciales cuyos clientes en su mayoría son hoy pequeños empresarios a un paso de la pobreza, asalariados y obreros. Así que, incluso el precio de la mercancía en el centro comercial (hoy para nosotros) oculta lo que la mercancía es, de verdad, es decir, su auténtico coste en dolor y sufrimiento, subsistiendo invisible en ella el mundo de opresión y relaciones humanas de dominación y explotación. Pero se da la circunstancia de que es en este mundo evitado y reprimido que nadie procura mirar donde realmente ocurre la historia y es el lugar donde la conciencia crítica imbuida y dinamizada por el sufrimiento es capaz de adivinar la “verdad”.
Un mundo que se ha desdoblado en un bello espejismo que constituye el ámbito de lo superestructural, es decir, la cultura. Las relaciones humanas impregnan la cultura, pero a menudo como negativos que dan la vuelta a las cosas, tornando bueno lo originariamente malo. Así, aunque parezca lo contrario, también en la dimensión cultural se nos priva de una vivencia que corresponda claramente con el modo de relaciones y el modo de vida al que se nos aboca. Si vivimos en y por ella, vivimos en la pura ilusión, en un ámbito fantasmal.
La realidad de tanta fantasmagoría es, en última instancia, la dominación, un modo de dominación social definido, que llega a constituir la verdad de las cosas, y que entre otros efectos ostenta el privarnos del carácter de libre acontecimiento de la existencia humana. Esta es restringida, puesta entre moldes y forzada a detenerse, a ser de un modo particular. Estamos lejos, claro, de concepciones que a fuer de comprender el poder, en cierto modo, lo naturalizan (aunque decir esto suene a barbaridad y sacrilegio, el aludir a lo natural entre quienes lo disuelven deconstructivamente); es decir, concepciones que convierten al poder en un fenómeno generalizado que la vida del hombre siempre va a padecer, ora para mal, ora para bien y que es cuestión de cómo se gestione en el microcosmos de las relaciones humanas y sociales, o en el macrocosmos de la razón política. Acaso también disuelvan estas ideas fuertes y monolíticas del poder, llenándola de matices, rasgos y circunstancias. Desde luego, estas corrientes filosóficas cercanas al postestructuralismo pueden acusar a la idea anarquista acerca del poder de ser la propia de actuales sectas gnósticas que no acaban de comprender y reconciliarse con la realidad humana, con lo fáctico, con lo que las cosas son. Y el anarquismo en su vertiente práctica, sobre todo, no puede aceptar bondad en poder alguno, en toda sus manifestaciones fenoménicas o incluso ontológicas. El poder es, como la estructura del Estado, un añadido que tapa la espontaneidad humana, la cual se opone, por tanto, a cualquier forma de dominación. Una especie de cobertura artificial que el hombre ha creado, sin estar determinado a ello. En fin, aludo a todo esto de un modo somero y rápido sin entrar por ahora en matices.
El materialismo de Benjamin parece suponer que el vínculo con el ser del concreto ser humano, entendido como “modo de ser” o “existencia”, se realizaría desde una perspectiva que está teñida de capitalismo. Su “definición” (o "humanización" en el término habitual de la pedagogía) se realiza en la historia que en la medida que se cosifica, cosifica al existente. Una invasión entificadora de lo ontológico, podemos adivinar titubeantes, que encorsetando y determinando a la historia, encorseta y cristaliza al hombre concreto. Una invasión en la que entran en juego factores como la tecnología (por ejemplo hoy asistimos a una redefinición del hombre, de lo humano, traída por internet, que implica un nuevo modo de ser aquello que llamemos “lo humano”). Este es, precisamente, el lado espantoso del mundo capitalista, la profundísima coacción a la libertad para que el hombre se autodefina entre lo espontáneo individual y colectivo.
Si trasladamos todo esto a la escuela, según Benjamin esta sería un entramado de ideales que ni se realizan ni estarán jamás realizados, que crea, literalmente, ese segundo mundo de la cultura que se enseña y que como una cortina va tapando de los ojos de los hombres lo que hay detrás de ello. Sería una función, como la que Marx atribuía a la religión, opiácea, por la que la escuela actuaría como una adormidera que nos haría creer que su mundo, el expresado en sus ideales, rituales, contenidos, pedagogías, es el verdadero, el bueno, y que el universo de los hombres se halla plagado de buenas intenciones y de justicia. Así, la escuela contribuiría al gran engaño del mundo capitalista, eliminando de sí todo elemento que responda a la realidad del trabajo y las relaciones entre los hombres en el mundo capitalista. Algo que comparten las explicaciones más pesimistas en torno al origen burgués e ilustrado de la institución escolar. En definitiva, un lugar donde se crea en gran medida al hombre desdoblado, mutilado y parcial que todos somos en la sociedad capitalista y que las experiencias socialistas en los antiguos países comunistas trataron de remediar, con mejor o peor fortuna, pero de manera sugerente y creativa que aún hoy deberíamos tener muy presente en la pedagogía (pronto nos dedicaremos a ello por aquí).
Este universo cultural de las ideas y valores es muy seductor y engancha, pues en él se vive como si fuera real la ilusión de un mundo diferente, justo, humano, altruista, generoso, pacífico. Pero el materialismo histórico de Benjamin trata de hallar una pedagogía alternativa que destaparía esta ideología, para dar la vuelta a todo, poniéndolo patas arriba, con el fin de que se visualice lo otrora invisible, es decir, la realidad, lo que ocurre de hecho en la historia y en la sociedad capitalista. En su libro sobre Benjamin, Susan Buck denomina a esto justamente una pedagogía materialista, que sería la que Benjamin emprende y aborda en muchas de sus obras, quedando expuesta en las Tesis sobre el concepto de historia. En ellas trata de “explicarse” (al modo críptico, asistemático y fragmentario que para Benjamin ha de asumir el lenguaje que trata de captar lo real) el proyecto del Libro de los Pasajes, mostrando esas verdades o realidades ocultas para nosotros, paseantes y compradores en un mundo ficticio cuya consistencia es apenas la de un sueño.
La verdad de la historia es, para Benjamin, la de la dominación y el final cruel de todos los sueños y utopías. Hay esta anticipación en la cultura burguesa que en momentos como los vividos en los pasajes parisinos puede manifestarse con estridencia en su naturaleza onírica. Es muy obvio que en el mundo ideal mostrado en ellos, se suspende el trabajo, la utilidad, el desdoblamiento entre lo público y lo privado, la explotación visible y que todo ello exulta en su carácter mítico. En el mundo capitalista se vive, como en la infancia, en un mundo de sueños, pero por mucho que estos parezcan ser sueños individuales de realización personal, la verdad es que no hay redención individual, salvo en un hipotético cielo de fantasmas, y que toda redención y origen de los deseos frustrados es histórica y colectiva. El niño capta en sus juegos el valor simbólico, mítico, que pueden adquirir los objetos, y juega con ello, lo presupone, lo inventa.
La importancia de las cosas menores para los niños imita lo que ocurre entre los adultos, es decir, la imposibilidad de limpiar de mito a la mirada. Así, en su exceso mitificador, el niño denuncia, inconsciente, lo que el mundo de los adultos está haciendo también con las cosas tornadas mercancías y objetos de deseo. El niño capta lo aurático y lo mítico con facilidad, en el paisaje urbano, por ejemplo. Alude Susan Bucks a textos autobiográficos de Benjamin en los que va señalando esto al hilo de sus recuerdos infantiles en Berlín. Pero el niño, en realidad, no inventa esto, sino que descubre el mito que con disimulo se desliza ante nuestros ojos en cualquier recoveco urbano del mundo capitalista. Un movimiento interpretativo que representa el primer paso para la redención. Es decir, en Benjamin hay un esfuerzo constante por desempolvar de mito a las cosas y desvelar, al mismo tiempo, la naturaleza de los sueños, su origen.
Lo que más difícil resulta de seguir en Benjamin es el modo en que, concretamente, se desarrolla esta pedagogía materialista, en palabras de Susan Bucks. Aquí una clave estaría en el mencionado Libro de los Pasajes. El esfuerzo filosófico del mismo estriba en destapar, justamente, lo onírico, haciendo que los objetos y las citas extraídas tanto de la gran literatura como del más variopinto universo de los textos desechables, prospectos, anuncios, informaciones útiles, edictos oficiales, periódicos, etc., al modo de fragmentos, si son puestas en relación, es decir, mostradas junto a otras citas de ya pasada y caduca utilidad, como relámpagos, iluminen constituyendo lo que Benjamin llamaba constelaciones, una imagen dialéctica en la que muchas veces se muestra lo oculto que a menudo contradice el propio significado de las citas tomadas individualmente. Así, las cosas y los mensajes encierran, oblicua y dialécticamente, su contrario. Se despierta el verdadero sentido de las citas, opuesto al significado literal. Una suerte de juego cabalístico (o incluso freudiano) tomado por Benjamin en su dimensión materialista, no teológica al modo de Scholen. Así, el saber al que podemos aspirar, acerca de nosotros mismos, irrumpe en lo fragmentario devastando la ilusión de la identidad o el mensaje directo, supuestamente, de las cosas.
Un fragmento da, pues, la clave, si se descontextualiza y se coloca en un nuevo universo compuesto por otros textos y fragmentos. Así, esforzadamente, se puede ir mostrando lo que está ocurriendo, abriéndose paso entre los sueños y fantasmagorías del mundo burgués. Y lo que hay detrás de tanto sueño vaporoso es la imposibilidad material de su realización. Es decir, una estructura que impide que todos los hombres se realicen es la que desata el deseo y su satisfacción simbólica en los márgenes irreales e inconsistentes de lo onírico. Los sueños van a constituir este universo ideal que solo se realiza en lo cultural y en las ideas. Pero al mismo tiempo hablará, aún más oculto, según una clave freudiana que Benjamin me parece que seguía, el carácter de pesadilla de nuestras vidas. Nuestros sueños son, pues, de dos tipos: ideales falsamente realizados como cultura y, también calladamente obvios, los que son pesadillas que expresan nuestra miseria como clase, es decir pesadillas de “barriga llena” o de “barriga vacía y de hambre”, señala Buck-Morss.
Mientras permanezcamos en este mundo burgués y en sus trampas, no habrá redención posible. Es lo que expresan sobrecogedora y contundentemente las Tesis sobre el concepto de historia. La historia, una vez se supera su modalidad onírica e ideológica, que es la que Benjamin denomina el “continuum”, no constituye un progreso ni una línea, no hay una única dirección, contra lo que estudiamos y leemos al intentar saber algo de ella, sino que también está teñida por lo fragmentario. En palabras de Benjamin, las "ruinas". Por eso, la historia que late por debajo del sueño del progreso, la historia real, es horrible, pues desarrolla antes bien el dominio, el engaño y la opresión, dejando como sedimento un vasto reguero de víctimas. Esto es lo que se ve por debajo del relato de los hechos. Así, Benjamin parece apuntar a algo semejante a lo que las deconstrucciones posestructuralistas de la segunda mitad del siglo XX y la actualidad llevan a cabo. Pero hay que percatarse bien de que el marxismo de Benjamin apunta a una verdad, una realidad que puede ser alcanzada y diferente ontológicamente del universo onírico y la falsa conciencia que se están disolviendo con cierto tono deconstructivo.
Hay, pues, en Benjamin un trabajo que hacer en lo cultural que, si tiene éxito, nos muestra una verdad. Pero para ello, y de ahí el genio revolucionario de Benjamin, hay que obrar un ruptura, llenar de grietas el continuum de la historia y el bien engarzado mundo onírico que, como en la película Matrix, todos creemos vivir como algo bueno, razonable, real, justo, obvio, etc. Un sueño al que contribuyen desde las leyes y el Estado, a, como hemos señalado, el relato de la historia (la historiografía y el historicismo) o el simbolismo onírico de las mercancías y toda la cultura que es propia de la sociedad de consumo. Es esta concepción pesimista y fragmentaria de la historia la que resulta propia de una aproximación revolucionaria a la misma, frente a las ideologías que de un modo u otro, incluida la socialdemocracia, justifican el carácter razonable y justo del todo, la posibilidad de una redención sin abandonar la estructura que constituye el infierno materializado al modo de la síntesis hegeliana, por ejemplo. Estas supuestas superaciones que se plantean desde la estructura de dominación y sin abandonarla, acaban confundiendo mito con realidad, igual que lo hizo el pensamiento ilustrado que se decía lo contrario de lo que era, y en la política actual, el liberalismo, la democracia cristiana o la socialdemocracia. También el marxismo clásico, a su manera continuista, del comunismo y del antiguo mundo soviético. Benjamin, como Freud, se va a fijar en los actos fallidos, en las asociaciones libres del pensamiento, en los sueños y su materia, para descifrar el mundo real que en ellos se insinúa oblicuamente y que ante estos ojos exentos de mito del historiador materialista, se alza como algo brutal, donde prácticamente nadamos en sangre y cuyos parciales bienestares, incluidos el disfrute de la alta cultura, presuponen un odio ciego y una dominación espantosa. La lectura de las famosas Tesis causa esta conmoción. Dicen algo impresionante, como una tormenta que de pronto revelara energías ocultas en la historia, discrepancias dialécticas existentes en el buen tiempo, apacible, de unos instantes antes de que estallara el relámpago. Pero esta pedagogía impregnada del sufrimiento (cuya memoria es mantenida, según expresa Benjamin en la conocida primera tesis del autómata que juega al ajedrez, por la teología, que da su “sentido”, de este modo lleno de negatividades y al estilo impugnador de la teología negativa, al materialismo histórico, obrando ella bajo él, y no al revés) es la única posibilidad de redención, colectiva, no individual, que, a un paso del abismo, de manera incierta y precaria, aún tenemos los seres humanos sin que nada esté garantizado. Hablamos de un saber negativo, como la teología. Los muertos siempre “estarán ahí”, clamorosos; y la historia, tal como la conocemos, no admite resolución alguna definitiva respecto a la carga de dolor que porta ni es posible tampoco aspirar a que sin más lo que ahora hay se supere algún día con una transformación cualitativa desde sí. Este es el "significado" oculto y silenciado de las víctimas.
Bibliografía:
Buck-Morss, S. (2014). Walter Benjamin. Escritor revolucionario. Buenos Aires: La Marca editora.
Se trata de un libro que contiene varios artículos de la gran estudiosa de Adorno, Benjamin y la primera generación de la Escuela de Fráncfort. Fueron publicados en torno a la primera edición crítica del Libro de los Pasajes a principios de los años ochenta, obra póstuma e incompleta de Benjamin que en español han editado recientemente Akal y Abada editores, que yo sepa.